Today I’m posting 2 problems relating to my student Dan Thornton’s independent study work.  I’m out of town this week and next, so I have these posts set to automatically go up on Tuesday afternoon.

Dan’s independent study was based on the “Automaton Identification” problem, but to show that reduction, he needs to use a variant of 3SAT, which he shows here:

The problem: Monotone EQ SAT. This is a specific instance of Monotone SAT.

The description:
We are given a conjunction of clauses where each clause in contains all negated or non-negated variables and the number of clauses and variables are equal, is there an assignment of the variables so that is satisfied? Our instance will have clauses and variables.

Example:
Here is an that has variables and clauses.

F =

The above may be satisfied by the following assignment:

The reduction:
We will reduce from Monotone SAT. So we are given an instance of Monotone  SAT with the clauses here each clause is of the form where each clause has all negated or non-negated variables. This is different from Monotone EQ SAT as we do not require the number of variables and clauses to be equal.
From this we must build an instance of Monotone EQ SAT.
We may transform our instance of Monotone SAT, , into one of Monotone EQ SAT by the following iterative procedure. New variables will be denoted by and new clauses by .

  = ;
 i = 1;
 j = 1;
 While{number of clauses != number of variables}{
   introduce two new variables ;
   If{number of variables  number of clauses}{
     Create the new clause ;
     ;
     ;
   }
   else {
     Create three new clauses:
      
      
      ;
     ;
     ;
   }
 ;
 }

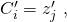
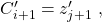
The above algorithm will produce an equation that is in Monotone EQ  SAT. This may be shown by induction. Notice that before the procedure if that we will add 2 new variables and 3 new clauses.

If then we will add 2 new variables but only a single new clause. Either way the difference between the number of variables and clauses, will decrease by . So in steps we will obtain an formula where = 0. Such a formula is an instance of Monotone EQ SAT.

True{Monotone SAT True{Monotone EQ SAT}
Here we assume that there is a truth assignment function that maps every variable to a truth value, such that is satisfied. Then after we preform the above algorithm we have an instance of , now our instance of will be of the form for some . Now notice that above will satisfy in and we may trivially satisfy by simply assigning all new variables to true.
This will give us a new truth assignment function that will satisfy

True{Monotone EQ SAT} True{Monotone SAT}
Here we assume that there is a truth assignment function that will satisfy then obviously as then must also satisfy .

(Back to me)

Difficulty: 3.  The logical manipulations aren’t hard, but it is possible to mess them up.  For example, it’s important that the algorithm above reduces the difference in variables and clauses by 1 each iteration.  If it can reduce by more, you run the risk of skipping over the EQ state.