Here’s the actual problem my student Dan Thornton spent most of his semester trying to understand and prove. It’s pretty crazy.
The problem: Automaton Identification from Given Data. We abbreviate it “AutID”. G&J call this problem “Minimum Inferred Finite State Automaton” and it is problem AL8 in the appendix.
The description: Given a finite set of data, is it possible to build a deterministic finite automata of 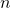 or fewer states that agrees with the data?
or fewer states that agrees with the data?
Prior to giving a description of this problem we must introduce a few concepts and definitions. We want to construct a finite automation, this means a Mealy model deterministic finite automata. Formally a 6-tuple of the form
![Rendered by QuickLaTeX.com \[FA = \langle U,S,Y,f_{tr},f_{out},s_{0} \rangle\]](https://npcomplete.owu.edu/wp-content/ql-cache/quicklatex.com-7f069676795dc1b2caa369ac4f8f2e28_l3.png)
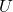 is the input alphabet, where
is the input alphabet, where 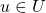 is an individual character, and
is an individual character, and 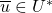 is a string.
is a string.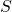 the set of states in the model.
the set of states in the model. 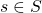 refers to an individual state.
refers to an individual state. 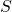 may equivalently be referred to as the set
may equivalently be referred to as the set ![Rendered by QuickLaTeX.com S_{[s]}](https://npcomplete.owu.edu/wp-content/ql-cache/quicklatex.com-b8150e1cdd7a6d8b6757709c274c72aa_l3.png) of all equivalence classes
of all equivalence classes ![Rendered by QuickLaTeX.com [s]_{\overline{u}}](https://npcomplete.owu.edu/wp-content/ql-cache/quicklatex.com-92de2112a12b2d8a768786943b94f7f2_l3.png) , with representative element
, with representative element 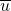 . Each equivalence class is a set of all input strings
. Each equivalence class is a set of all input strings 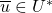 such that
such that 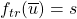 .
. the output alphabet, where
the output alphabet, where 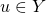 is a individual character,
is a individual character, 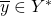 .
.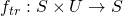 is the transition function.
is the transition function.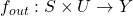 is the output function.
is the output function.
- Both of the above functions may be extended in a natural way so that
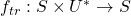 and
and 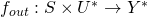 respectively. Usage should be clear from context.
respectively. Usage should be clear from context.
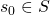 is the start state.
is the start state.
We use the standard convention that 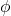 refers to the empty string of no characters.
refers to the empty string of no characters.
A black box is similar to an ‘unknown’ Mealy model with the restriction that for any input string 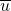 we only get to see the last output character
we only get to see the last output character 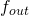 returns. Consider the following black box. With input alphabet
returns. Consider the following black box. With input alphabet 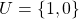 and output alphabet
and output alphabet 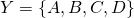 .
.
Here the edges are labeled 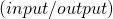
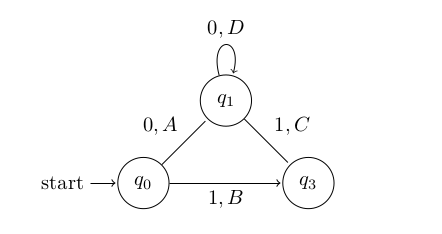
So if the above known black box was passed the string 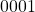 the complete Mealy model’s output function would give us back the string
the complete Mealy model’s output function would give us back the string 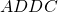 where as the black box would only give us back
where as the black box would only give us back 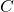 .
.
Now our above finite automata is constructed using data we are given, here we assume that data is a set 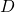 of finite pairs of the form
of finite pairs of the form 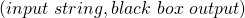 .
.
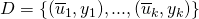 such that
such that 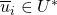 is not empty and
is not empty and 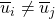 for
for 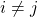 .
.
An automata 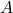 agrees with data
agrees with data 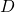 if for every datum
if for every datum 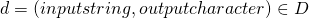 , the final output character of
, the final output character of 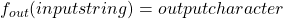 .
.
Formal Problem Statement:
Given input alphabet 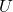 , output alphabet
, output alphabet 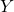 and data, a set
and data, a set 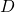 of finite pairs determine if an automation of
of finite pairs determine if an automation of 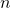 or fewer states exists that agrees with D.
or fewer states exists that agrees with D.
The Reduction:
The reduction by Gold uses Monotone EQ SAT. So we are given a conjunction of clauses 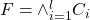 where each clause in
where each clause in 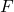 contains all negated or non-negated variables
contains all negated or non-negated variables 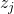 and the number of clauses and variables is equal, is there an assignment of the variables so that
and the number of clauses and variables is equal, is there an assignment of the variables so that 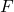 is satisfied? Our instance will have
is satisfied? Our instance will have 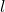 clauses and variables. Clauses will be numbered
clauses and variables. Clauses will be numbered 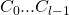 and variables will be numbered
and variables will be numbered  .
.
In the above instance of Monotone EQ SAT we do not have a variable 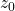 . Indices in our reduction will sometimes force us to reference
. Indices in our reduction will sometimes force us to reference 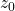 . We may think of this variable as simply a place holder for
. We may think of this variable as simply a place holder for 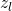 .
.
The idea behind this reduction is that we may encode our instance of Monotone EQ SAT into data 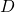 in such a way that if we can create a finite automata from our encoding, then we can use it to obtain a solution to the instance of Monotone EQ SAT if one exists.
in such a way that if we can create a finite automata from our encoding, then we can use it to obtain a solution to the instance of Monotone EQ SAT if one exists.
Aut ID construction:
Here we transform our instance of Monotone EQ SAT into data 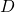 , to do so we need the following functions:
, to do so we need the following functions:
![Rendered by QuickLaTeX.com \[I_{F}(i,k) = \left\{ \begin{array}{ll} "no-value" & \quad \text{ if }\ z_{l - k} \in C_{i} \\ 0 & \quad otherwise \end{array} \right. \\ \text{where } \\ 0 \leq i \leq l-1 \text{ and } \\ 1 \leq k \leq l\]](https://npcomplete.owu.edu/wp-content/ql-cache/quicklatex.com-db17321b6b612335215b2b83e316bbda_l3.png)
![Rendered by QuickLaTeX.com \[\pi_{F}(i) = \left\{ \begin{array}{ll} 1 & \quad \text{if}\ C_{i} \text{ contains uncomplemented variables}\ \\ 0 & \quad \text{if}\ C_{i} \text{ contains complemented variables}\ \end{array} \right. \\ \text{where } \\ 0 \leq i \leq l-1\]](https://npcomplete.owu.edu/wp-content/ql-cache/quicklatex.com-a6fbe6efd8964306d5c4206c9444899d_l3.png)
The bounds on the above functions are a result of our numbering of clauses 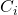 and
and 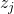 . Note that
. Note that 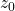 is really a placeholder for
is really a placeholder for 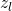 .
.
Given a propositional formula 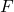 which is an instance of MonotoneEQ SAT we encode it by the following:
which is an instance of MonotoneEQ SAT we encode it by the following:
- The variables of
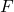 are encoded by the set
are encoded by the set
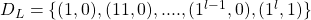 . Here each
. Here each 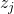 corresponds to the element
corresponds to the element 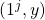 where
where 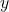 is an element of the output alphabet,
is an element of the output alphabet, 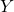 .
.
- We encode the clauses
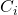 of
of 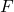 by
by 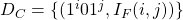 for
for 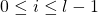 ,
, 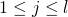 . Here each clause has a \textit{identifying tag},
. Here each clause has a \textit{identifying tag},  , then the
, then the  term is used specify a particular variable,
term is used specify a particular variable, 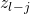 . Importantly, datum in this set for which
. Importantly, datum in this set for which 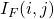 returns
returns 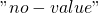 are thrown out.
are thrown out.
- Each clause encoding
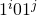 will be
will be 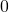 only if clause
only if clause 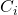 does not contain variable
does not contain variable 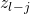 , otherwise
, otherwise 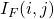 will be
will be 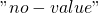 and is thrown out.
and is thrown out.
- We then encode whether each clause is a set of all negated, or non-negated variables.
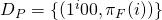 for
for 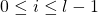 .
.
As a simple example we convert to data the following formula
![Rendered by QuickLaTeX.com \[F = (z_{1} \vee z_{2} \vee z_{4}) \wedge (\neg z_{2} \vee \neg z_{3} \neg z_{4})\]](https://npcomplete.owu.edu/wp-content/ql-cache/quicklatex.com-e84b8a203e829b8c5d81789477dd7231_l3.png)
So after our conversion we get:
Aut ID instance
Now we create an instance of 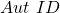 by letting
by letting 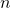 be the number of variables
be the number of variables 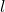 and
and  .
.
True{Aut ID} 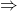 True{Monotone EQ SAT}
True{Monotone EQ SAT}
Now we may assume that we have a finite automata 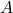 that agrees with the data in
that agrees with the data in 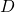 . Now we may use the transition function
. Now we may use the transition function 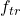 and the output function
and the output function 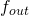 to deduce properties of
to deduce properties of 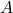 .
.
Let 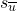 be
be 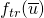 , this is the state that
, this is the state that 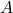 is in after receiving the input string
is in after receiving the input string 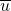 .
.
A splitting string of 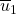 and
and 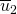 is a string
is a string 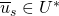 so that
so that 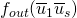 differs from
differs from 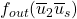 . If such a string exists then obviously
. If such a string exists then obviously 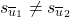 . If two states do not have splitting string then they are equivalent
. If two states do not have splitting string then they are equivalent
We define variable states as follows, a variable 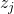 has the encoding
has the encoding 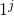 , so
, so 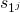 is
is 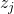 ‘s variable state, we will sometimes refer to this as
‘s variable state, we will sometimes refer to this as 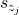 .
.
Clause states are defined in a manner similar to variable states. A clause 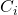 corresponds to the identifying tag in the encoding of
corresponds to the identifying tag in the encoding of 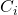 or
or 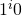 , so
, so 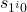 is
is 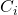 ‘s clause state, we will sometimes refer to this as
‘s clause state, we will sometimes refer to this as 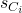 .
.
In the following theorems we shall talk of assignment of clause state 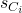 to variable state
to variable state 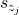 , this means that these two states are equivalent or alternatively that there does not exist a splitting string of
, this means that these two states are equivalent or alternatively that there does not exist a splitting string of 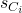 and
and 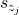 .
.
Theorem 1:All variable states are different.
Proof. We assume two variable states are equal 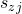 and
and 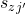 where
where 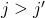 . Then in the encoding of
. Then in the encoding of 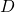 we get
we get 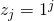 and
and 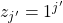 respectively. But now we may define the splitting string
respectively. But now we may define the splitting string 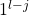 . The final element of
. The final element of 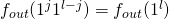 is defined in our data
is defined in our data 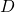 as
as 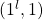 . By a similar argument we get
. By a similar argument we get 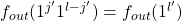 where
where 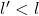 , in our data this corresponds to one of the entries
, in our data this corresponds to one of the entries 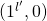 . Our automata
. Our automata 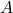 must agree with the data, so as a result these states
must agree with the data, so as a result these states 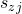 and
and 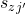 cannot be equal. Thus we have reached a contradiction.
cannot be equal. Thus we have reached a contradiction. 
Theorem 2: Each state in our finite automata 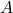 corresponds to exactly one variable.
corresponds to exactly one variable.
Proof. The above follows by the pigeonhole principle, as 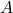 has exactly
has exactly 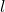 states, there are
states, there are 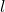 variable states, and by Theorem 1, no two variable states are equal.
variable states, and by Theorem 1, no two variable states are equal. 
By the above we may talk about the states of 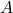 in term of the variable each state corresponds to.
in term of the variable each state corresponds to.
Theorem 3: If clause state 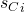 and variable state
and variable state 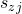 are equal, Then clause
are equal, Then clause 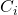 contains variable
contains variable 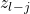 .
.
Proof. Assume 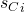 =
= 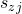 and
and 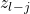 is not contained in
is not contained in 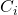 . Once again we have the following encodings
. Once again we have the following encodings 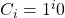 and
and 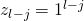 that were defined in our construction of
that were defined in our construction of 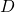 . Now we may define a splitting string
. Now we may define a splitting string 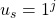 . When we append the splitting string to each of the above encodings we get
. When we append the splitting string to each of the above encodings we get 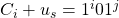 and
and 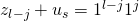 . Both of these strings are defined in our data
. Both of these strings are defined in our data 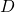 as
as 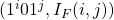 and
and 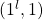 respectively, and by our assumption that
respectively, and by our assumption that 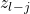 is not contained in
is not contained in 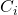 ,
, 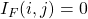 So by the a conclusion identical to that of Theorem 1,
So by the a conclusion identical to that of Theorem 1, 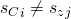 and our theorem follows.
and our theorem follows. 
Theorem 4:No two clause states 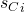 and
and 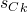 may be equal if they are of opposite composition, meaning one has all negated variables, and the other all un-negated variables.
may be equal if they are of opposite composition, meaning one has all negated variables, and the other all un-negated variables.
Proof. Once again we proceed by contradiction, assume 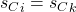 and that
and that 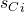 ,
, 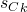 are of opposite composition. Once again we get each clauses encoding
are of opposite composition. Once again we get each clauses encoding 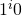 and
and 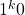 respectively. Now we may define the splitting string
respectively. Now we may define the splitting string 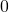 . Looking at the final character output by
. Looking at the final character output by 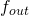 we see
we see 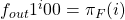 and
and 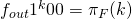 . It follows that
. It follows that 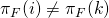 as
as 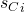 and
and 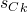 are of opposite composition. Thus we arrive at a contradiction.
are of opposite composition. Thus we arrive at a contradiction.
Theorem 5: 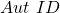 gives us a solution to
gives us a solution to 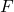 our instance of
our instance of 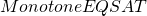 .
.
Proof. By Theorem 2 every clause state must be assigned to a single variable state, notice this does not mean only a single assignment is possible but just the given automata 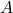 will give a single assignment. By Theorem 1 no clause may be assigned more than one variable state. By Theorem 3 a clause may be assigned to a variable state only if the clause contains the variable. So we see that our automata
will give a single assignment. By Theorem 1 no clause may be assigned more than one variable state. By Theorem 3 a clause may be assigned to a variable state only if the clause contains the variable. So we see that our automata 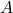 assigns clauses to the variables that could potentially satisfy them. Furthermore by Theorem 4, each variable state is given clauses of only one composition, so there is an obvious variable assignment to satisfy all of the clause states equal to a given variable state.
assigns clauses to the variables that could potentially satisfy them. Furthermore by Theorem 4, each variable state is given clauses of only one composition, so there is an obvious variable assignment to satisfy all of the clause states equal to a given variable state. 
True{Monotone EQ SAT} 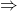 True{Aut ID}
True{Aut ID}
Now we assume there exists a mapping 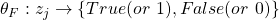 that satisfies our instance of Monotone EQ SAT,
that satisfies our instance of Monotone EQ SAT,  with
with 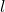 clauses and variables. From this mapping we build a finite automata
clauses and variables. From this mapping we build a finite automata 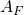 that agrees with all data
that agrees with all data 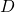 .
.
We let 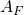 ‘s 0-transitions refer to transitions on input 0. Similarly 1-transitions refer to the transitions on input 1.
‘s 0-transitions refer to transitions on input 0. Similarly 1-transitions refer to the transitions on input 1.
So first we define all 1-transitions as given in the following example automata, obviously such transitions will satisfy all data in 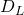 .
.
Now for  to satisfy all of the data in
to satisfy all of the data in  we notice by Theorems 3 and 4 above mapping each clause to the variable state that satisfies it seems like a natural thing to do. We may determine this mapping of clauses to the variables that satisfy them from our truth assignment that satisfies
we notice by Theorems 3 and 4 above mapping each clause to the variable state that satisfies it seems like a natural thing to do. We may determine this mapping of clauses to the variables that satisfy them from our truth assignment that satisfies 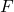 ,
, 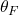 .
.
Such mappings may be added to 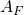 by noticing the following, as soon as we encounter a 0 in input we must transition to a clause state. So we may define a 0-transition for every state in
by noticing the following, as soon as we encounter a 0 in input we must transition to a clause state. So we may define a 0-transition for every state in 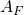 that maps the clause state
that maps the clause state 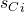 (which recall corresponds to the string
(which recall corresponds to the string 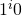 ) to the variable state
) to the variable state 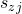 that satisfies it. When adding 0-transitions we must be careful as if clause
that satisfies it. When adding 0-transitions we must be careful as if clause 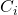 is satisfied by variable
is satisfied by variable 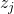 then in order to agree with the data in
then in order to agree with the data in 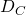 we really should map
we really should map 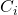 to variable
to variable 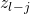 due to the definition of
due to the definition of 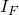 .
.
Now we must assign an output to each of these 0-transitions. To do so we iterate through every clause state 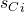 by sequentially considering
by sequentially considering 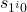 . At each clause state we assign the output of the 0-transition starting at this state to be
. At each clause state we assign the output of the 0-transition starting at this state to be 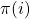 . Notice that if two clause states
. Notice that if two clause states 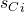 and
and 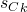 are identical, then they must both be satisfied by the same variable and so therefore
are identical, then they must both be satisfied by the same variable and so therefore 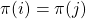 .
.
Below is an example of adding such a 0-transition and assigning its output:
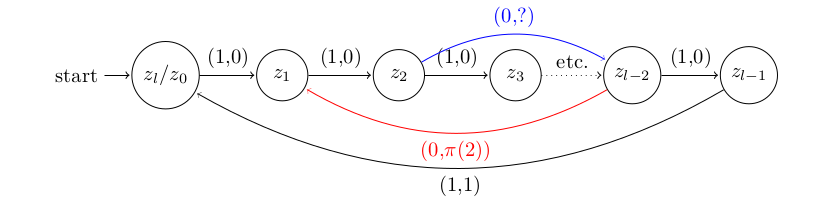
The Blue edge is the zero transition added that maps the clause state 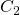 ,which corresponds to the string
,which corresponds to the string 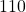 , to the variable state
, to the variable state 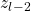 . Semantically this means that the variable
. Semantically this means that the variable 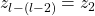 satisfies this clause.
satisfies this clause.
The Red edge shows us adding the output value of a 0-transition, as from the above blue edge we know 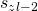 corresponds to the clause
corresponds to the clause 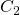 ‘s clause state, so to the zero transition from this clause state will have output
‘s clause state, so to the zero transition from this clause state will have output 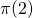 .
.
Theorem 6: Our constructed automata 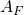 agrees with all
agrees with all 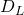
Proof. This is quite obvious from our example of 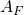 in Figure 1. We have defined all the
in Figure 1. We have defined all the 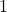 transitions, and notice that the final output of all
transitions, and notice that the final output of all 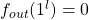 if
if  and
and 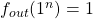 this exactly matches our data
this exactly matches our data 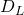 .
. 
Theorem 7: Our constructed automata 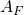 agrees with all
agrees with all 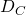
Proof:Here we consider the final character output of 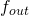 for all encodings of fixed clause
for all encodings of fixed clause 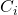 , these encodings are precisely the
, these encodings are precisely the 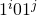 for
for 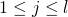 . Now with the addition of the
. Now with the addition of the 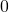 -transitions, we transition into
-transitions, we transition into 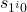 , and from this state we only worry about
, and from this state we only worry about 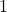 -transitions. Recall that in our definition of
-transitions. Recall that in our definition of 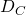 , all datum are of the form
, all datum are of the form 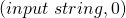 . In
. In 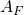 there is a single
there is a single 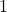 -transition that outputs the non-zero value
-transition that outputs the non-zero value 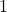 . To agree with
. To agree with 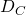 it is sufficient to make sure that this non-zero output occurs for an input string not in
it is sufficient to make sure that this non-zero output occurs for an input string not in 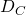 .
.
From our assignment of 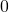 -transitions defined above this singular
-transitions defined above this singular 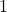 -transition that outputs
-transition that outputs 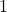 will occur for the variable
will occur for the variable 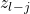 that satisfies
that satisfies 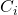 , so then
, so then 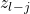 must be in
must be in 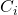 . So
. So 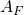 will give the datum (
will give the datum (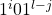 ,1). Now notice the corresponding entry in
,1). Now notice the corresponding entry in 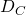 as defined by
as defined by 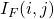 would be (
would be (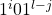 ,
,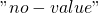 ), but all of these datum were removed from
), but all of these datum were removed from 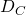 . So the sufficiency condition above is satisfied.
. So the sufficiency condition above is satisfied. 
Theorem 8 :Our constructed automata 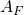 agrees with all
agrees with all 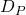
Proof: The manner in which we defined our 0 transitions explicitly involved a 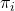 term, so for any clause state
term, so for any clause state 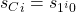 , now a 0 transition as defined above will output
, now a 0 transition as defined above will output 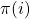 which will obviously agree with
which will obviously agree with 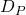
By Theorem 6, Theorem 7, and Theorem 8. We conclude that 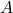 will agree with data
will agree with data 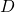
(Back to me)
Difficulty: 9. This is basically the reduction in the Gold paper, though Dan reorganized it a bunch to make it fit our format, and be more understandable. But the formatting of the various variables, the fact that you need to define the IF function on variable k to talk about zl-k instead of zk, and the three different kinds of test data all make this super hard to understand. In some ways, I wonder if this should be a 10, given the work we did on it. But I’m saving the 10’s for things that are truly impenetrable, and we did manage to figure this one out.
![]() where each clause in
where each clause in ![]() contains all negated or non-negated variables
contains all negated or non-negated variables ![]() and the number of clauses and variables are equal, is there an assignment of the variables so that
and the number of clauses and variables are equal, is there an assignment of the variables so that ![]() is satisfied? Our instance will have
is satisfied? Our instance will have ![]() clauses and variables.
clauses and variables.![]() that has
that has ![]() variables and
variables and ![]() clauses.
clauses.![]()
![]() may be satisfied by the following assignment:
may be satisfied by the following assignment:![]()
![]()
![]()
![]()
![]() here each clause is of the form
here each clause is of the form ![]() where each clause has all negated or non-negated variables. This is different from Monotone EQ SAT as we do not require the number of variables and clauses to be equal.
where each clause has all negated or non-negated variables. This is different from Monotone EQ SAT as we do not require the number of variables and clauses to be equal.![]() we must build an instance of Monotone EQ SAT.
we must build an instance of Monotone EQ SAT.![]() , into one of Monotone EQ SAT by the following iterative procedure. New variables will be denoted by
, into one of Monotone EQ SAT by the following iterative procedure. New variables will be denoted by ![]() and new clauses by
and new clauses by ![]() .
.=
; i = 1; j = 1; While{number of clauses != number of variables}{ introduce two new variables
; If{number of variables
number of clauses}{ Create the new clause
;
;
; } else { Create three new clauses:
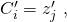
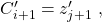
;
;
; }
; }
![]() that is in Monotone EQ SAT. This may be shown by induction. Notice that before the procedure if
that is in Monotone EQ SAT. This may be shown by induction. Notice that before the procedure if ![]() that we will add 2 new variables and 3 new clauses.
that we will add 2 new variables and 3 new clauses.![]() then we will add 2 new variables but only a single new clause. Either way the difference between the number of variables and clauses,
then we will add 2 new variables but only a single new clause. Either way the difference between the number of variables and clauses, ![]() will decrease by
will decrease by ![]() . So in
. So in ![]() steps we will obtain an formula where
steps we will obtain an formula where ![]() = 0. Such a formula is an instance of Monotone EQ SAT.
= 0. Such a formula is an instance of Monotone EQ SAT.![]() True{Monotone EQ SAT}
True{Monotone EQ SAT}![]() that maps every variable to a truth value, such that
that maps every variable to a truth value, such that ![]() is satisfied. Then after we preform the above algorithm we have an instance of
is satisfied. Then after we preform the above algorithm we have an instance of ![]() , now our instance of
, now our instance of ![]() will be of the form
will be of the form ![]() for some
for some ![]() . Now notice that
. Now notice that ![]() above will satisfy
above will satisfy ![]() in
in ![]() and we may trivially satisfy
and we may trivially satisfy ![]() by simply assigning all new variables
by simply assigning all new variables ![]() to true.
to true.![]() that will satisfy
that will satisfy ![]()
![]() True{Monotone SAT}
True{Monotone SAT}![]() that will satisfy
that will satisfy ![]() then obviously as
then obviously as ![]() then
then ![]() must also satisfy
must also satisfy ![]() .
.

