Monthly Archives: January 2016

This problem makes me think about how voting districts are apportioned, and how we can use algorithms to solve real-world situations like gerrymandering.

The problem: Bounded Component Spanning Forest.  This is problem ND10 in the appendix.

The description: Given a graph G=(V,E) where each vertex has a non-negative weight, and two integers K and B, can we partition the vertices of V into K (or less) disjoint subsets where each subset is connected and the sum of the weights of the vertices in each subset is at most B?

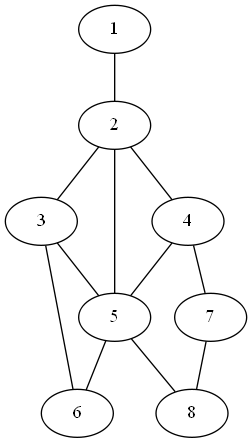
Example: Here’s a graph where each vertex is labeled with its weight.  Note that in this example, the edge weights are distinct and sequential, and that doesn’t have to be the case.

If K=3 and B = 14, then we can partition this into {1,2,4,7}, {5,8}, and {3,6}.  If K=3 and B=10, this can’t be solved. (The vertices 8 and 7 would have to each be in their own set, because anything they connect to would raise the total of that set beyond 10, and the sum of all of the other vertices is more than 10.  So we need more than 3 sets to partition the vertices if each subset needs to be a connected set with total weight 10 or less)

Note: Here’s how this applies to the voting problem I alluded to above.  Each congressional district is made up of several “precincts”- local areas that have a smallish number of people.  The boundaries of each congressional district is a connected group of wards.  So, for example, I’m part of Ohio’s 12th congressional district, but even within the relatively small town I live in, there are at least 3 different precincts, and I have a specific one assigned to me.

We could apply the Bounded Component Spanning Forest problem to this situation by creating a graph, where each vertex in the graph represents a precinct and has a weight equivalent to the number of people living in that precinct.  Two precincts have an edge between them if they’re geographically adjacent.  We can be given a list of all of the precincts in the state, and then K would be the number of congressional districts to form.  B would be a bound on how large (in terms of number of people) each district can be (or, how far from 1/Kth of the population each district can be).  This works in creating congressional districts, and, as we’ll see, is already NP-Complete, even before thinking about gerrymandering.

The only requirement so far is that each district has to be contiguous- nothing has yet been said about the shape.  But a natural definition of “non-gerrymandered” could be “minimum diameter”, and so we can add a new parameter, D, to the problem, and force each of the K subsets of vertices to not only be connected, but be connected with diameter D or less.  Since this is a generalization of the original problem, this is also NP-Complete (by a difficulty 1 reduction).

So, there you go.  Fixing gerrymandering (at least by this definition) is NP-Complete.  Since most states have hundreds (perhaps more- it’s remarkably non-trivial to find a simple answer to “how many precincts are in Ohio”) of precincts, the best we could likely do is some heuristic mechanism, and of course, any heuristic has a chance of being suboptimal against one party or another, and so they will never accept it.  Sigh.

Anyway, back to the math!

The reduction: From Partition into Paths of Length 2.  We’re given a graph G that needs to be partitioned into paths of length 2.  Recall that a path of length 2 has exactly 3 vertices, and that an instance of this problem promises that the number of vertices is a multiple of 3.

We’ll use the same graph for our Bounded Component Spanning Forest instance, and set K=|V|/3, give each vertex weight 1, and set B=3.

Now, each set of our partition has to be connected and have exactly 3 vertices, which is the same as having a path of length 2.

Difficulty: 2.