The other major reduction my student, Dan Thornton, was working on was a reduction for the old NES Pokemon game.

This is Dan’s last reduction for his independent study class.  He’s going to be applying to grad schools this year- if you’re running a grad program, you should accept him!

(Over to Dan)

The Problem:
Here we prove that a generalized version of the classic Pokemon Red/Blue video game is NP-complete.  Generalized Pokemon(hereafter referred to as ) asks the following question: Given a party of Pokemon and a map of trainers, can you get from the start position to the end position without having all of your Pokemon defeated in battle and continue your journey of catching them all?

This is based off of a paper by Aloupis, Demaine, Guo, and Viglietta on classical Nintendo games.

Background:
The goal of any Pokemon game is progress through the world collecting all Pokemon to become the very best Pokemon trainer there ever was. For more background see this link. We will focus on a subproblem where there is a path filled with enemy trainers from a start point to some end point. Solving and determining if we can get to the finish from the start turns out to be NP-complete.

In our construction of , there are two types of enemy trainers we will encounter, Hard trainers which we will always lose against, and Easy trainers which we will always win against. The details of this construction will be described below.

The description:
Here we reduce from 3 SAT by building certain constructs or gadgets in that can be used to model clauses, variables, variable assignment, and satisfiability. Then inductively using these component pieces we may build an instance of that is logically equivalent to one from . Below is the framework that we will map components of on to.

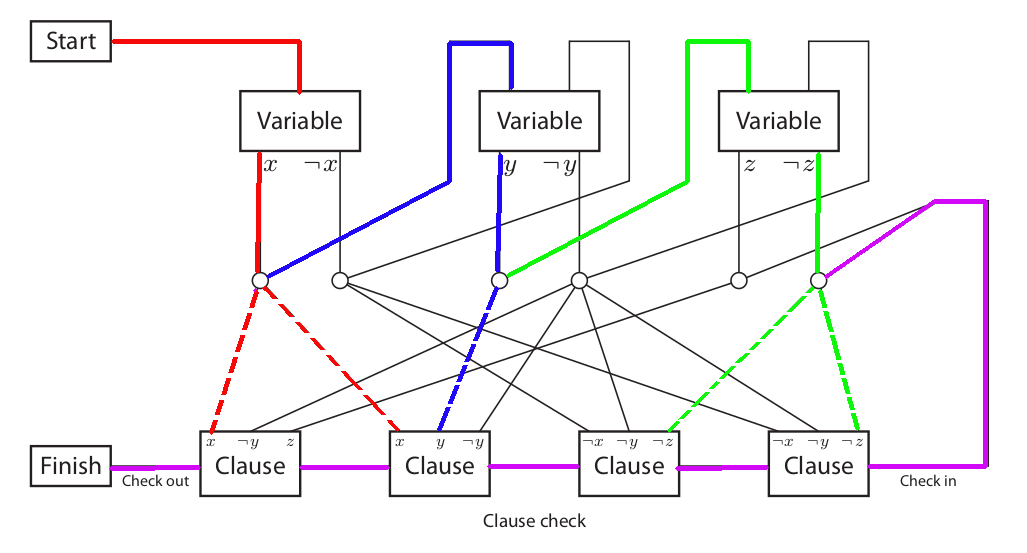
In the above figure all solid lines are single use paths, all dashed lines have no traversal limit.

The idea is that our trainer starts at the Start location and proceeds to a variable gadget, they then have an exclusive choice between two paths. One path reflects the assignment of true, the other of false. This choice will take us to a series of paths that will let us proceed to each clause the variable assignment satisfies and unlock it. Then we move on to the next variable. Eventually after proceeding through all of the variable clauses, we arrive at the Check in phase. Here we try to pass through all of the clauses, only the clauses we previously satisfied with the correct variable assignment may be passed through. Now if all clauses are satisfied, then we are able to pass through every one and arrive at the Finish state.

As an example in the above figure the colored edges give use a path that will satisfy all the clauses and pass to the Finish. The red edges show us assigning the value of true to then proceeding to the first and second clause which are satisfied by this assignment of . The blue edges show an assignment for and the green one for . It is important to note that we are unable to move backwards except on dashed edges, this prevents us from going back and attempting to correct our variable assignment.

Introduction
To show equivalence we break any instance up into to following: . Here each clause is of the form:
where

and each is a literal of the form .

Components

The construction of the GP instance is built out of several component pieces,  each described below.

Trainer Construction

Our trainer has a single Pokemon, a Ghastly that knows only a single move– Self-Destruct, a move that when used causes the user to faint but deals massive damage to a single enemy Pokemon. If it is ever our trainer’s turn during a battle we are forced to use a move.

By the above, if we ever use a move, we lose due to us only having a single suicidal move and a single Pokemon. When we lose we are unable to move and will be unable to get to the Finish.

Hard trainers have two Snorelaxs, both of which are slower than our Ghastly, so when we go into battle against them we are forced to use self-destruct and lose. Even if we cause a single of the opponent’s Snorelax to faint we still lose the battle as they have another.

Easy trainers all have a single Electrode that only knows self-destruct and has more speed than our Ghastly, so they will always go first and destroy themselves. Now normally self destruct would also deal massive damage to our Ghastly but, because Ghastly is a ghost type Pokemon, and self-destruct is a normal type move, it will not effect our Ghastly. Thus the opposing trainer will run out of Pokemon before us, and we win.

So, we have a situation where we may encounter any number of weak trainers and win, but a battle with a strong trainer guarantees a loss.

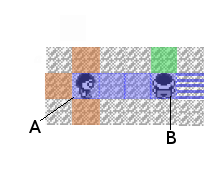
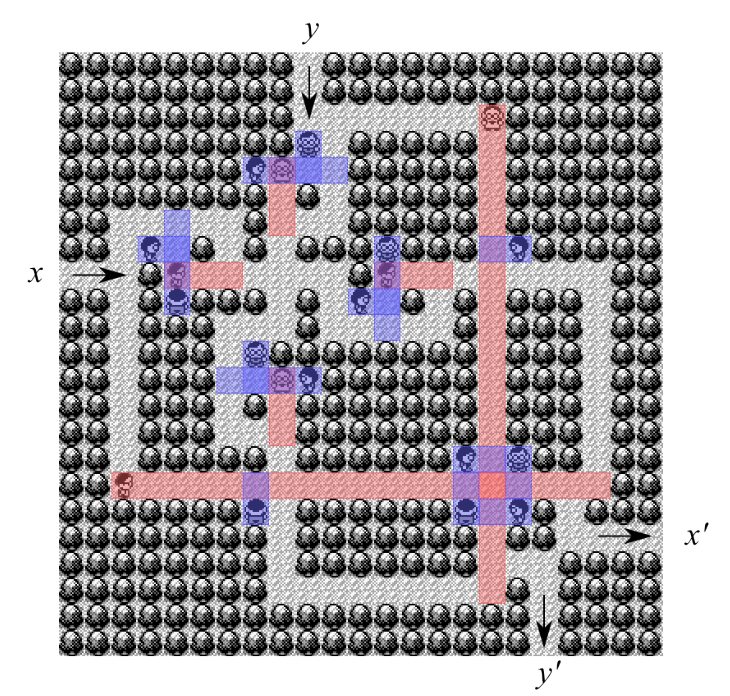
Field of Vision

Enemy trainers have a “field of vision” of some fixed length. In the above Figure, Player A’s field of vision is given by all blue squares. Once a player enters a trainer’s field of view they will be unable to move, the enemy trainer who can see them will approach and the trainer will be forced to battle. Other enemy trainers can block a trainer’s field of view, for example the striped blue box above is no longer in trainer A’s field of view due to trainer B.

Alternatively, we may choose to force an enemy trainer to battle our trainer if we stand in any of the orange squares.

Finally, once an enemy trainer has been defeated they will remain on the square they were defeated on indefinitely, so if we challenged and beat trainer A with our trainer standing on any of the orange squares, then trainer A would stay on the exact square he is on even if our trainer moved into his field of vision (any of the solid blue squares).

To distinguish the two types of trainers hard trainers will have a blue field of vision, whereas easy trainers will have a red one.

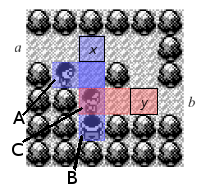
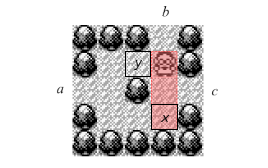
Variable Construction
Variable assignment may be modeled using the construction in Figure 3. Here the player enters through a. The player may either choose to move to battle the enemy trainer while standing on square x or y. If our trainer battles the enemy trainer on square x then the enemy trainer will block off the c exit, and once defeated will stay there indefinitely. Alternatively if our trainer battles on square y then the defeated enemy trainer will remain where he is indefinitely and we must exit through c. So this construction therefore presents the player with an exclusive choice between two possible paths b or c.

 

Single Use path
In order to prevent a player from re-tracing his or her steps to access previous paths we may use the construction below. Here if we assume a player enters from a and will exit through b.

Notice that to pass from a to b our player must pass through both squares marked x and y. Notice that once we pass through y trainer C will have moved forwards to battle our trainer at y. This now means that trainer B has line of sight to x. Now because we must go through x square to get from a to b or b to a any passage through this gadget will be impossible.

Also notice that if we enter from b then we must pass through y before x and so by the same argument as above this is impossible.

Trainer A simply serves as a barrier from letting us battle trainer C from an adjacent square.

So this gadget is a single use unidirectional path.

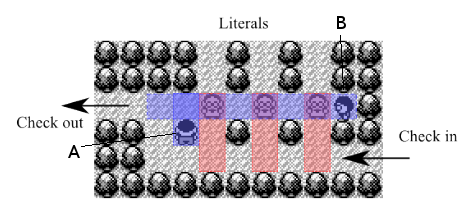
Clauses
Below we illustrate a clause, each of the weak trainers is a literal.
If the player at any time enters through any of the three literal paths from above, then they may battle a weak trainer. If a player battles any of the weak trainers then later on when the clause gadget is entered through check in then the weak trainer the player already battled will not approach the player, and will instead continue to block hard trainer B’s field of vision so that we may pass through to check out. Hard trainer A is there just to prevent re-entering the literal clauses after entering this gadget through check in.

Crossover
The crossover gadget shown below is present to deal with the issue of planarity, as there is no device in the original Pokemon games for passing “over” other portions. Then if we view the paths between gadgets as edges of a graph similar to our framework in the first figure, then without this gadget we are restricted to building planar graphs.

This gadget lets two paths cross without letting a player switch the path they are on. So if you enter from a player is forced to leave through and similarly for and . Each path is single use, but using the ‘s path, has no effect on our use of the ‘s path and vice versa.  As a result we may assume we can build a single use path between any two points.

 

Reduction
Here we reduce from an instance of . We are given a formula with the form defined in section 4. Now we build into an instance of using the reduction framework in Figure 1 as well as our components. We also impose the restriction that in every variable gadget path corresponds to assigning a literal the value and corresponds to .

If we have a variable assignment that satisfies then by definition there is a literal in every clause such that satisfies . Then in our constructed instance of we must be able to visit the literal section of every clause gadget at least once prior to arriving at the check-in phase. So it follows that we are able to battle at least 1 of the easy trainers in each clause gadget before check-in. Therefore it must be possible for us to reach the finish.

If it is possible for our trainer to get from start to finish, then again by the framework in Figure 1 we must be able to battle an easy trainer in each of our clause gadgets. To reach these clause gadgets the trainer had to make an exclusive decision in each variable gadget. This choice corresponds to a literal assignment. So the path our trainer takes through the variable gadgets, and then through the clause gadgets to the finish gives us an assignment of literals such that every clause is satisfied. Obviously this corresponds to an assignment that satisfies .

(Back to me)

Difficulty: 9.  This isn’t that hard to understand, but there are lots of details that are needed- having to position the trainers in exactly the right position for it all to work.