I feel a little silly I didn’t come up with this one myself.
The problem: Clustering. This is problem MS9 in the appendix.
The description: Given a complete weighted graph G=(V,E), with a positive weight d(i,j) for each edge eij, and two positive integers K and B. Can we partition V into K (or less) disjoint sets V1..Vk such that within each Vi, all edges that stay within the partition cost B or less?
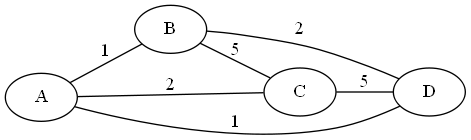
Example: Here is a graph:
If K=2, and B=2, we could have the sets {A,C} and {B,D} as a legal cluster. But if K=2 and B=1, we will not be able to solve the problem. For example, we might want to have the edges (A,B) and (A,D) in the same cluster, but that would require us also to consider the edge (B,D), which is larger than 1.
Reduction: Brucker’s paper introduces the problem using a graph, like I did above. (G&J talk about points and distances), His reduction is from Graph Coloring.
Suppose we have a coloring graph G. We build a new graph G’ such that the weight of an edge in G’ is 1 if it did not appear in G, and its weight is 2 if it did appear in G. Then we set out K = the K of the coloring problem (3 for 3-coloring), and B = 2. A partition of the vertices into 3 sets where each set has no weight-2 edges is exactly a legal coloring.
Difficulty: 3. I do think the graph terminology helps to make the problem more understandable.