This is one of my favorite problems, but one of the worst reductions to understand. I usually skip over it when I teach it, showing them the picture of the widget and saying “See? It’s Nuts!” and moving on
The problem: Hamiltonian Circuit (HC)
The definition: Given a graph G=(V,E), where |V| = N. Can I create an ordering <v1, v2…vn>of the vertices where an edge exists between each (vi, vi+1) in the sequence, and the edge (vn, v1) also exists?
(In other words, does a sequence of edges exist that lets me start at some vertex, visit each other vertex exactly once, and return to the start?)
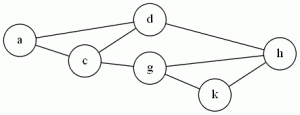
Example:
The sequence <a,d,h,k,g,c> forms a Hamiltonian Circuit
The reduction: Is from VC, and it’s nuts. G&J do it on pages 56-60. Starting with an instance of VC (A graph G, and an integer K), build a new graph G’ with:
- K “selector” vertices (a1-ak)
- 12 vertices and 14 edges (see page 57) for each edge in G (a “cover-testing” component
- Edges to connect the selector vertices to the start and end of the cover-testing component.
The Cormen algorithms book has an example of this, and it takes a graph with 4 vertices and 4 edges and builds a HC instance with 50 vertices and 72 edges.
Difficulty: 9, only because I’m sure there exist reductions that have like 25 page proofs, and I want to save my 10 for that. But really, I think just making the students trace this reduction on an example is a really hard problem.
I like the reduction from 3-SAT and I find that students have no trouble following it.