Back to the “core 6” with a classic problem from graph theory. There are lots of similar graph problems, so it’s important to keep them all straight.
The Problem: Vertex Cover (VC)
The Definition: Given a graph G=(V,E) and a positive integer K (G&J say that K ≤ |V|, but really, if it’s bigger than that, you can have the algorithm just return “yes”). Can I find a subset V’ of V, |V’| ≤ K, where every edge in E has at least one endpoint in V’?
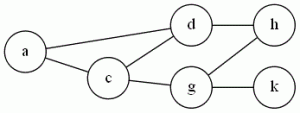
Example: Hmm, I wonder if I can insert an image..
Ok, looks like that worked. In the graph above, {c,d,g} is a vertex cover, because all edges have at least one endpoint in the set {c,d,g}. As we’ll see later, a graph containing a clique (complete subgraph) of N nodes will need at have at least N-1 of those vertices in the cover.
The reduction: From 3SAT. G&J on pages 54-56 show the construction. We build a graph with vertices for all variables and their negation, with an edge between them. We have three variables for each clause, connected in a triangle. (The three variables correspond to “positions” in the clause). Then there is an edge from each vertex corresponding to a literal (or its negation) to its corresponding “clause vertex”- the vertex that holds the position of that variable in the original formula. K= # of variables + 2* number of clauses.
Difficulty: 7 , assuming it’s the first time a student has seen this sort of reduction. If they have seen something similar (for example, a reduction from 3SAT to Clique), then maybe a 5. The ideas are pretty similar.
Note: I teach my algorithms class using the Cormen book. In it, they reduce 3SAT to Clique, proving Clique is NP-Complete, and then reduce Clique to VC. This works in the exact same way as the reduction from VC to Clique that I’ll be doing here next.