The last of the three similar graph problems, it’s also probably the easiest reduction.  When I teach NP-Completeness, I’ve had a lot of success starting with this reduction (instead of building a stable of NP-Complete problems from zero like the textbooks do).  You kind of have to say “Trust me, Vertex Cover is NP-Complete, I’ll show you why later”, but starting with a simple reduction means that they can follow the idea and the process right from the beginning without having to be bogged down in ugly conversions involving SAT.

The problem: Independent Set (IS)

The definition Given a graph G=(V,E) and an integer J.  Does G have a collection of at least J vertices where no edges connect any two vertices in J?

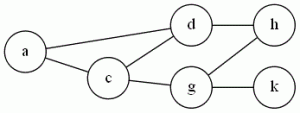
Example:  Using the same graph:

{a,h,k} is an independent set of size 3.

The reduction: From VC.   Use the exact same graph, and set J=|V|-K.  (G has an independent set of J vertices exactly when it has a vertex cover of K vertices.  Vertices not in the cover can’t have edges between them).

Difficulty: 1.  There’s a reason why I do this first (though sometimes I go from Clique instead).  In general, though, I try to avoid making them do problems that are too easy for homeworks and tests.  If the reduction is trivial, it makes showing that the conversion solves the original problem difficult.  You get a lot of proofs that basically say “C’mon!  They’re the same thing!”.  Which is not what I’m looking for 🙂