G&J don’t even bother to prove Clique is NP-Complete, just stating that it (and Independent Set) is a “different version” of Vertex Cover. But the problem comes up often enough that it’s worth seeing in its own right.
The problem: Clique (I’ve also seen “Max Clique” or “Clique Decision Problem” (CDP))
The definition: Given a graph G=(V,E), and a positive integer J (G&J say J needs to be ≤ |V|, but I think you can allow large values and make your algorithm just say “no”). Does J contain a subset V’ of V, or size at least J, where every two vertices in V’ are joined by an edge in E?
Example: Using the graph we had for VC:
{a,c,d} form a clique of size 3. There are no cliques of size 4, but if we add the edge (d,g) and the edge (c,h), then the vertices {c,d,g,h} would be one.
The reduction: From Vertex Cover. Given a graph G and an integer K that is an instance of Vertex Cover, take the complement of G (the complement of a graph has the same vertices, but the set of edges is “inverted”: (u,v) is an edge in the complement if and only if it was not an edge in G), and use it as your instance of CDP. Set J= |V|-K
Difficulty: 3. It’s not a 2 because it takes a little thought to see why the complement works.
Note: As stated perviously, I teach this course using the Cormen book, so in class I show Clique is NP-Hard by reducing from 3SAT. It’s a good example of a hard reduction, probably about as hard as the VC reduction G&J do.
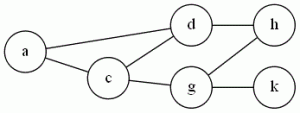
There are no cliques of size 4, but if we add the edge (d,g), then the vertices {c,d,g,h} would be one.
It would be right if we have two edges (d,g) and (c,h).
oops, I’ll fix it now. Thanks!