Tag Archives: uncited reduction

Maximum Likelihood Ranking

Leave a reply

This is another (hopefully the last, we’re getting close to the end) “private communication” problem where I couldn’t find a paper to use, so I had to work through it myself, with mixed success.  Let’s see how I do.

The problem: Maximum Likelihood Ranking.  This is problem MS11 in the appendix.

The description: Suppose we have an nxn matrix A with integer values.  Further, let aij + aji = 0.  We’re also given a positive integer B.  Can we do “simultaneous row and column permutations” to A to create another matrix (G&J call it B, but I’ll call it C to avoid confusion), such that:

\sum_{1 \leq i < j \leq n} min\{b_{ij},0\} \geq -B?

The description (my interpretation): Here’s what I think that means.  You have a directed  graph with just one edge in each direction between any 2 vertices, represented as an adjacency matrix  A positive entry in the matrix is the cost to traverse the edge, and a negative entry in the matrix means you’re traversing the edge backwards.  Can I permute the rows and columns of the matrix so that the “backwards” edges in all positions where i < j sum to -B at most?”

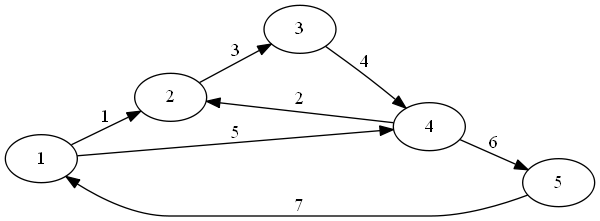
Example: Here is a graph:

Here is its matrix:

\begin{bmatrix} 0&1&0&5&7 \\ -1&0&3&-2&0\\ 0&-3&0&4&0\\ -5&2&-4&0&6\\ 7&0&0&6&0\\ \end{bmatrix}

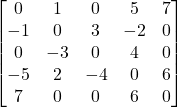
The negative numbers in the upper right triangle is what we are looking at to compare against our B- in this case it’s -9.

I’m pretty sure a “simultaneous row and column permutation” means you do the same permutation to the rows and to the columns.  So if the above matrix was {1,2,3,4,5}, here is {2,3,4,5,1}

\begin{bmatrix} 0&3&-2&0&-1\\ -3&0&4&0&0 \\ 2&-4&0&6&-5 \\ 0&0&-6&0&7\\ 1&0&5&-7&0\\ \end{bmatrix}

The negatives in the upper right triangle here sum to -8 (so it’s better).  It’s worth noticing that we have two cycles in the graph (2->3->4->2 and 1->4->5->1), and that any permutation will have to have a “backwards” ordering for one of the cycles.  So at least 1 edge in each cycle will have its negative value counted in our total, so this graph will be at least -7.

(Partial) Reduction: As I said, this is a “private communication” reduction, our only hint is that we are supposed to use Feedback Arc Set.  What Feedback Arc Set asks for is a set of edges that is in each directed cycle.

So, let’s try this:  Given a directed graph G=(V,E) that’s our Feedback Arc Set graph, represent it as an adjacency matrix such that aij = 1 if edge (i,j) is in E, and aij = -1 if (j,i) is in E.  Our B will be the K from the problem.

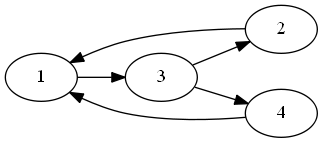
My intuition is that each cycle will have to contribute 1 edge (at least) that is negative in our upper triangle.  So if there are K edges that cover all cycles, we would get the B cost from those edges in our problem.  We want the edge in the feedback arc set to be last in the permutation order.  For example, here is a directed graph:

Here is its graph with the regular ordering:

\begin {bmatrix} 0&-1&1&-1\\ 1&0&-1&0\\ -1&1&0&0\\ 1&0&0&0\\ \end{bmatrix}

..for a cost of -3.  But we can solve the FBS instance with just 1 edge from 1-3.  So here is the matrix will all edges going forward except for that one (3,2,4,1 ordering):

\begin{bmatrix} 0&1&1&-1\\ -1&0&0&1\\ -1&0&0&0\\ 1&-1&0&0\\ \end{bmatrix}

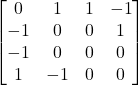
..for a cost of -1 (because there is just 1 edge in the Feedback Arc Set)

I’d like to have my reduction be someting like “put all edges in the Feedback Arc Set in the matrix in order where they go backwards”.  But I don’t know what to do with graphs like this, where the Feedback Arc Set itself is a cycle, so you can’t do that:

{(3,4), (4,6), (6,3)} is the Feedback Arc Set here, but because it is itself a cycle, there is no permutation of vertices that will put all of the edges in the upper right.  I think this is a consequence of there being 4 cycles in the graph, but the Feedback Arc Set having just 3 edges.  But I’m not sure, and so we need to have something more in the reduction.

Difficulty: ??  It doesn’t look terribly hard, but I’m not sure what to do next.

Randomization Test For Matched Pairs

Leave a reply

This reduction gave me a lot of trouble and gave me a lot of holes to fill.  I think I filled them okay, but I’m getting the vibe that I’m missing something here- the reduction reads very differently from the way the problem is described.

The problem: Randomization Test For Matched Pairs.  This is problem MS10 in the appendix.

The description: Given a series of n pairs of integers (x1, y1) through (xn, yn), and a positive integer K.  Are there at least K subsets of the integers for which:

\sum_{i \in S} |x_i - y_i | \leq \sum_{y_i > x_i} (y_i - x_i)?

Example:  The paper by Shamos that has the reduction might have a better explanation of what we are doing: he defines zi = yi – xi, and T* to be the sum of all of the positive zi (the right side of the inequality above).  Then if we could choose some set of zi to be positive (by changing their sign), and call that sum T, are there K or more sets where T \leq T*?

So, suppose we have 4 pairs: (2,4), (1,6), (8,4), (3,2).  This would make our zi‘s {2,5,-4,-1}, and so T* would be 7.

There are 16 subsets of the above pairs (nothing seems to say that the empty set isn’t allowed).  Here are some whose T is \leq 7:

{(2,4), (1,6)}   (T=7)

{(2,4), (8,4)} (T=6)

{(2,4), (8,4), (3,2)} (T=7)

{(3,2)} (T=1)

..and so on.  A set that does not work is {(1,6), (8,4)} since its T is 9.

Reduction: Shamos uses Partition, so we are given a set of N elements.  The total sum of the elements is S, so we want two subsets of size S/2. He wants to “Perform the randomization test on the numbers” in the partition set, which I don’t get because the test needs to be done on pairs.  He also wants T* to be S/2.  The paper seems to say that you can just set that, but it has to be based on the zi.  So I came up with a way to make that happen:

For each item xi, create a pair  (xi, 0).  The zi for each of these elements will be negative.  Then add one extra pair (0. S/2).  Since this is the only positive z value, T* will be this value.  I don’t know if this is what the paper wants me to do, and I’m a little worried that adding an extra element will throw off what is next.

The paper then claims that if there is no partition of the set elements into equal-weight subsets, there are 2N-1 subsets with a T < T*.  This is because if there is no partition of equal size, then each subset of our elements either has a sum < S/2 (and this a T < T*), or its complement does.

If there is a partition, then 2 sets will have a T value of exactly T* (the two partition subsets) and half of the remaining subsets will have a T < T* as above.  So if we set K (the number of subsets whose T needs to be <= T*) to be 2N-1+2, we will have our reduction.

Difficulty: 7. I spent a long time trying to read and understand this reduction.  It’s very sparse, and, really, doesn’t explain at all how to make the pairs.  As a result, I’m pretty sure I filled in all of the holes, but it’s very possible that I’m missing something.