Tag Archives: Difficulty 6

Minimum Weight And/Or Graph Solution

Leave a reply

This is a cool, fun reduction.  I also teach And/Or graphs in my Artificial Intelligence class, so it was fun to see this as a problem here.

The problem: Minimum Weight And/Or Graph Solution.  This is problem MS16 in the appendix.

Description: An And/Or graph is a directed, acyclic graph, where each vertex is marked as either an “and” node, or an “or” node.  We’re given a start vertex, s.  Then we “solve” the subtree at s by:

  • Solving all children of s, if s is an “and” node,
  • Or, solving one child of s, if s is an “or” node.

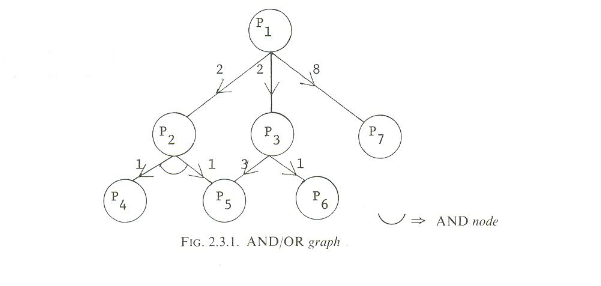
The solution proceeds recursively, until we get to a leaf, which can be solved directly.  Here is an example from the paper:

So, to solve P1, we could solve either P2, P3, or P7.  To solve P2, we’d need to solve both P4 and P5.

In this problem, the edges are weighted, and we’re asked: Given an integer K, is there a solution that traverses edges costing K or less?

Example: In the graph above, the cheapest solution costs 3: Solve P1 by solving P3, solve P3 by solving P6.  If P3 was an “and” node, instead of an “or” node, then the best solution would cost 4: Solve P1 by solving P2, solve P2 by solving both P4 and P5.

Reduction: Sahni’s paper has a bunch of reductions we’ve done.  This time, he uses 3SAT.  So, from a given 3SAT instance, we build a graph:

  • S is the root node, and is an “and” node
  • S has one child for each variable (x1..xn).  There is also one extra child, P.
  • Each xi is an “or” node with 2 children, one for “true”, one for “false”.   (So 2n children total)
  • Each of these 2n nodes have 1 edge coming out of it to one of the 2n leaves of the tree.
  • P is an “and” node, and has one child for each clause (C1..Ck).
  • Each clause node is an “or” node, and has 3 edges corresponding to its literals.  So if variable xi appears in clause Cj positively, there is an edge to the “true” child of xi.  If the negation ~xi appears, there is an edge to the “false” child of xi.
  • The weights of each edge are 0, except for the 1-degree edges going to the leaves, which cost 1.

To solve this graph, we need to solve S, which means we need to solve each variable (by “choosing” a truth setting for it), and we also need to solve P.  Solving P means we need to solve each clause.  Each clause is solved by choosing a truth setting for one of its literals that makes the clause true.  Since we are already choosing a truth setting for each variable, we are paying N in cost.  If we can choose setting of the variables that also solve each clause, we pay no more than N in cost, and also satisfy each clause.  If the formula is unsatisfiable, then we need to solve one variable “twice” by setting it to true and false, making us pay more than N overall.

So the formula is satisfiable if and only if the tree cost is exactly N.

Difficulty: 6.  I don’t know that I’d expect a student to come up with this themselves.  It is similar to a lot of the 3SAT reductions we’ve done, though (one “thing” per clause, one “thing” for each variable setting, connections between the clause and the settings of its literals), so if a few of these were gone over with students, maybe this could be presented along with them.

 

Decision Tree

Leave a reply

We teach decision trees in our AI and Data Analytics classes, so this is a nice problem that relates to that.

The problem: Decision Tree.  This is problem MS15 in the appendix.

The description: We’re given a set X of n objects, and a set T of tests.  Each test can be applied to each object, and returned true or false.  Can we arrange tests so that after at most K tests, we uniquely identify all objects in X?

Example: A decision tree is a way to take an unknown object and classify it into one of the elements of X.  So suppose X= {1,2,3,4}  We’ll have 3 tests:

Test 1: Is it even?

Test 2: Is the value of the number < 3?

Test 3: Does the spelling of the word have < 4 letters?

Then we could write this decision tree of height 2:

We could also use the same test in multiple nodes.  The decision trees I come across also allow for the same object from X to appear in many different leaves (because X is usually a boolean set like {Yes, No}), but the definitions here don’t seem to allow that.

Reduction: The paper from Hyafil and Rivest uses X3C.  So we’re given a set of elements X, and a collection C of 3-element subsets of X.  We’ll build a set X’ (the objects of the decision tree problem) by taking X and adding 3 new elements: {a,b,c}.  We will have 1 test in T for each triple in C (“Is our object one of these 3 elements?”).  We’ll also have 1 test for each element x in X’ (“Is our object x?”).

The paper defines a formula that we are trying to minimize for the height of the tree:

f(n) = \min_{1 \leq i \leq 3} [f(n-i) + f(i) + n] if n \geq 4

f(1) =2, f(2) = 2, f(3) = 5, f(4) = 8

So our K is f(|X’|).

We’ll want the optimal tree to look like this (picture from the paper):

The nodes in the tree above are 3-element sets from C that form the cover.  So the first node is asking “Is X in the first set of the cover?”.  If the answer is yes, we move to the right, and use the 1-element tests to figure out which of the 3 leaf nodes correspond to the exact element.  If the answer is no, we move to the left, and ask the same question of the second set in the cover.  The way to minimize the tree’s height is to have the “what 3-element set” questions be first.  We also minimize the height by making sure that each element of X’ is covered by a node in the tree- in other words, the T_{i_k} sets have to form a cover.  This means we get the minimum height (of K) from the tree if and only if we have a cover from C.

Difficulty: 6.  The reduction itself isn’t hard, but the formula is hard to see, and the paper kind of handwaves the “of course you need to be an exact cover” part of the proof.  I think if students had to do it, they’d run into some sticky issues.

Programs With Formally Recursive Procedures

Leave a reply

This is the last of the “Program Optimization” problems, and the next section is the last one on “Miscellaneous” problems, which has 19 problems in it.  So, unless some diversion into a problem not in the book happens, we’re on the countdown through the last 20 problems!  The end is in sight!

The problem: Programs with Formally Recursive Procedures.  This is problem PO20 in the Appendix.

The description: Given a set of function definitions and a program that makes a sequence of function calls using those definitions (the paper by Winklmann uses Algol because he wrote it in 1982.  But any language that allows recursion should work).   Are any of the procedures in the program formally recursive?  For our purposes, “formally recursive” means that there exists a chain of calls that has a call to a function higher in the chain (not necessarily a parent, any ancestor will do).

My first instinct was to wonder if this problem was actually undecidable.  It’s not because we will have some fixed # of procedures d, and so any call chain needs to be checked only to depth d+1- if we get that far, we must have a repeat someplace.  If we never get that far, we can back up and check other call chains, eventually checking all of the paths through the call tree exhaustively.  The proof that the problem is in NP is in the paper, but it involves representing the call tree as a DAG so we can use one vertex for two equivalent paths.  Winklmann says that if you do that the number of vertices is “bounded” by the number of procedures in the program (he doesn’t say what that bound is, though).

Example: It’s hard to make a small example that’s not obvious.  How about this:

E(){
  E();
}

D(){
}

C(){
 A();
}

B(){
 D();
}

A(){
 B();
 F
}

main(){
  A()
}

If “F” is replaced by a call to C, the program is formally recursive, because the call chain main->A->C->A has a repeat.  If we replace that F with another call to B the program is not formally recursive because even though recursive functions like E exist (and even though B gets called twice in two different chains), there is no call chain that will start at main and hit E (or anything) more than once.

Reduction: Winklmann uses 3SAT.  So we start with a formula B with m clauses and n variables.  We’ll write some functions:

AssignXi(c1..cm): generates two calls to AssignXi+1. The function has one parameter for each clause.  The first call simulates setting variable Xi to true by passing a “true” value in all parameters that represent clauses that have variable Xi represented positively.  The second call simulates setting variable Xi to false by passing a “true” value in all parameters that represent clauses that have variable Xi returning negatively.  In all other cases, the function passes on the ci parameter it was given.

AssignXn(c1..cm): once we reach the end of the variables, we have to stop.  This function calls the “Check” function we’ll be defining in a minute twice, once reflecting setting variable Xn to true, one reflecting setting it to false.

Truej(cj+1..cm):There is one “true” function for each clause, each one has a parameter for all clauses with larger numbers. The paper writes this function a little weirdly, but I think a good definition is:

if(cj+1 is true){
Truej+1(cj+2..cm);
else
Falsej+1(cj+2...cm);
}

So, as long as the parameters are true, we’ll continue calling down through the  true functions to the end.  The last True function is what will make us formally recursive:

Truem(): Calls Assign1(False, False, ...False). Our main program will begin with a call to Assign1 with these exact parameters, so if we can get here, we will have found our recursive call.

The False functions end a call chain:

Falsej(cj+1..cm){
// do nothing
}

The Check function’s job is to start the appropriate call to True or False:

Check(c1..cm){
if(c1 is true)
True1(c2..cm);
else
False1(c2..cm);
}

Our main program is just a call to Assign1(False, False..False).  It’ll go through all of the various AssignXifuntions trying to assign variables (and thus clauses) to true. Each assignment will be checked, and each check will either hit a False function (meaning a clause wasn’t satisfied, and so we will backtrack and try an alternate assignment) or the final True function, which will generate our recursive call.  So this program has a recursive call chain if and only if the formula was satisfiable.

Notice that while the run of this program might take exponential time, that’s ok because reductions are concerned with the time it takes to create the new problem instance, and there are “just” 2m+n+1 functions to create.

Difficulty: 6.  This is a neat problem and reduction- I think the “write a backtracking program to try all combinations” is pretty gettable.  The hard part is the check and true/false functions at the end.  We can’t really use loops because loops make programs undecidable (you can’t show the problem is in NP by going down d+1 calls if you might have an infinite loop someplace and won’t get through all of those calls).  So we have to build a chain of recursive calls instead, with dead-ends to force the backtracking.