I told Daniel when he gave me his Monotone Satisfiability reduction that the actual problem mentioned in G&J was Monotone 3-Satisfiability. So he went off and did that reduction too.
The Problem:
Monotone 3 SAT. This is a more restrictive case of Monotone SAT
The Description:
Given an formula of clauses 
where each clause in 
contains all negated or non-negated variables, and each clause 
contains at most 
variables. Does there exist an assignment of the variables so that is satisfied?
Example:
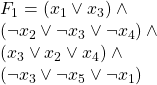
the following assignment satisfies 
:
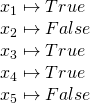
However:
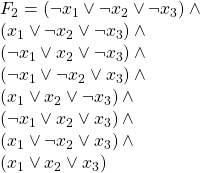
And the following is 
in Monotone 3SAT form:
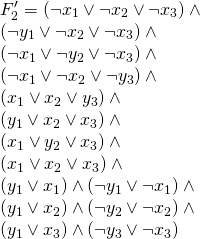
are both unsatisfiable.
The reduction:
In the following reduction we are given an instance of 3SAT,
. Here each clause is of the form:
where
and each 
is a literal of the form 
.
We use the following construction to build an instance of Monotone 3 SAT out of the above instance of 3SAT :
In each clause we have at most one literal, 
that is not of the same parity as the rest of the literals in the clause. For every such literal, we may preform the following substitution:
this yields a modified clause 
.
Now we must be able to guarantee that 
and 
are mapped to opposite truth values, so we introduce the new clause:
and conjunct it onto our old formula 
producing a new formula .
For example:
so we preform the substitution
so 
and 
Now repeating this procedure will result in a new formula: 
.
We claim logical equivalence between the 
and 
This is semantically intuitive as the 
clause requires all substituted literal in to take the value opposite of this was the stipulation for the substitution initially. It is also verifiable by truth table construction for:
:
If there exists a truth assignment 
that satisfies , then we may extent this truth assignment to produce 
which will satisfy
by letting 
for all 
and letting 
for all .
Obviously if is satisfiable 
must be by the above construction of . So by the above claim we have that will satisfy .
:
Continuing from the above, if we have a truth assignment 
that satisfies , then by the claim above it also must satisfy . And is a sub-formula of so any truth assignment that satisfies must also satisfy .
(Back to me)
Difficulty: 4, since it’s a little harder than the regular Monotone Sat one.
Is this even more restrictive version of Monotone 3-SAT (Monotone 2-3 SAT) too NP-Complete:
1. All Clauses are monotone.
2. All positive monotone clauses are of length 3.
3. All negative monotone clauses are of length 2.
I don’t know, I haven’t heard of that variant. Let’s think about it.
The reduction above gets you most of the way to where you want to go, with 2 exceptions:
1) The transformation can create a positive monotone clause of length 2
2) The original F may have a negative monotone clause of length 3.
Of these, the second one worries me the most. Since 2-SAT is polynomial, we know that there isn’t a way to (in polynomial time) convert a set of clauses of length 3 into an equivalent set of clauses of length 2. (Because if we could, we’d have a reduction from 3SAT into 2SAT and P=NP). It seems like you’d have to do something like that to make this case work.
So my gut feeling is that it’s not NP-Complete. but it’s possible that there is a different clever reduction out there that would do it.
Why can’t we use the same reduction as monotone SAT here?
Well, the monotone sat reduction doesn’t assume that we have clauses of 3 literals. And it doesn’t build a new clause that has 3 literals either.
But it is true that once we have this 3-sat reduction, Monotone SAT is automatically NP-Hard.