Tag Archives: Difficulty 4
Protected: Integral Flow With Multipliers
Monotone 3-Satisfiability
I told Daniel when he gave me his Monotone Satisfiability reduction that the actual problem mentioned in G&J was Monotone 3-Satisfiability. So he went off and did that reduction too.
The Problem:
Monotone 3 SAT. This is a more restrictive case of Monotone SAT
The Description:
Given an formula of clauses ![]() where each clause in
where each clause in ![]() contains all negated or non-negated variables, and each clause
contains all negated or non-negated variables, and each clause ![]() contains at most
contains at most ![]() variables. Does there exist an assignment of the variables so that
variables. Does there exist an assignment of the variables so that ![]() is satisfied?
is satisfied?
Example:
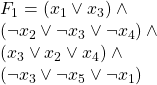
the following assignment satisfies ![]() :
:
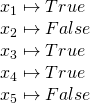
However:
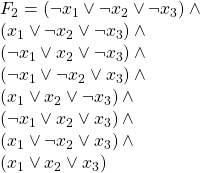
And the following is ![]() in Monotone 3SAT form:
in Monotone 3SAT form:
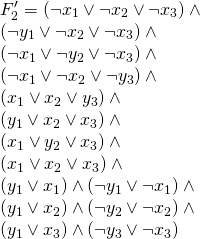
are both unsatisfiable.
The reduction:
In the following reduction we are given an instance of 3SAT,
![]() . Here each clause is of the form:
. Here each clause is of the form:
![]() where
where
![]()
and each ![]() is a literal of the form
is a literal of the form ![]() .
.
We use the following construction to build an instance of Monotone 3 SAT out of the above instance of 3SAT :
In each clause ![]() we have at most one literal,
we have at most one literal, ![]() that is not of the same parity as the rest of the literals in the clause. For every such literal, we may preform the following substitution:
that is not of the same parity as the rest of the literals in the clause. For every such literal, we may preform the following substitution:
![]() this yields a modified clause
this yields a modified clause ![]() .
.
Now we must be able to guarantee that ![]() and
and ![]() are mapped to opposite truth values, so we introduce the new clause:
are mapped to opposite truth values, so we introduce the new clause:
![]() and conjunct it onto our old formula
and conjunct it onto our old formula ![]() producing a new formula
producing a new formula ![]() .
.
For example:
![]() so we preform the substitution
so we preform the substitution
![]()
so ![]() and
and ![]()
Now repeating this procedure will result in a new formula: ![]() .
.
We claim logical equivalence between the ![]() and
and ![]() This is semantically intuitive as the
This is semantically intuitive as the ![]() clause requires all substituted literal
clause requires all substituted literal ![]() in
in ![]() to take the value opposite of
to take the value opposite of ![]() this was the stipulation for the substitution initially. It is also verifiable by truth table construction for:
this was the stipulation for the substitution initially. It is also verifiable by truth table construction for:
![]()
![]() :
:
If there exists a truth assignment ![]() that satisfies
that satisfies ![]() , then we may extent this truth assignment to produce
, then we may extent this truth assignment to produce ![]() which will satisfy
which will satisfy
![]() by letting
by letting ![]() for all
for all ![]() and letting
and letting ![]() for all
for all ![]() .
.
Obviously if ![]() is satisfiable
is satisfiable ![]() must be by the above construction of
must be by the above construction of ![]() . So by the above claim we have that
. So by the above claim we have that ![]() will satisfy
will satisfy ![]() .
.
![]() :
:
Continuing from the above, if we have a truth assignment ![]() that satisfies
that satisfies ![]() , then by the claim above it also must satisfy
, then by the claim above it also must satisfy ![]() . And
. And ![]() is a sub-formula of
is a sub-formula of ![]() so any truth assignment that satisfies
so any truth assignment that satisfies ![]() must also satisfy
must also satisfy ![]() .
.
(Back to me)
Difficulty: 4, since it’s a little harder than the regular Monotone Sat one.
Protected: Stacker-Crane
Protected: Rural Postman
Protected: Network Survivability
Protected: Network Reliability
Weighted Diameter
It took over a year (the first problem strictly from the Appendix was Domatic Number, last August), but we’re finally at the end of the Graph Theory section! And the last problem is one that’s actually good for students to solve.
The problem: Weighted Diameter. This is problem GT65 in the appendix
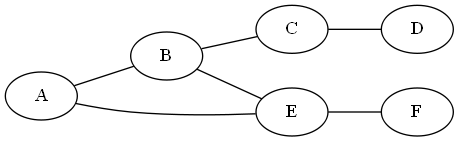
The description: Given a graph G=(V,E) a collection C of |E| not necessarily distinct, non-negative integers, and a positive integer K. Can we find a one-to-one function f mapping each edge in E to an element of C such that if f(e) is the length of edge e, then G has a diameter of K or less.
In other words, given a set of edge weights C, can we give each edge in E a (distinct) weight from C such that the resulting weighted graph has a path between any two vertices of length ≤ K?
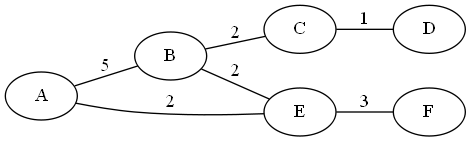
Example: Suppose I have a graph:
And C= {1,2,2,2,3,5}. I think the best was you can label this is:
The Diameter here is 7 (The length of the path from A-D).
The reduction: G&J say to use 3-Partition, so we’ll go with that. We’re given a set A, with 3m elements, a bound B, and want to split the elements of B into sets of size 3 so that each set adds up to m. We know several things about A, but the important thing for our purposes is that all of the elements in A add up to m*B.
We’ll also assume that |A| is at least 9. If it’s smaller than that, we can just brute-force the answer.
What we’re going to do is build a graph that is a tree with 3m+1 vertices. We have a root, and the root has m chains of length 3 extending from it. This gives us exactly 3*m edges.
We set K = 2*B, and set C = A
If there exists a 3-partition of A, then each of the sets of 3 elements can map onto a different chain in the graph. This makes the longest path in the graph be between any 2 leaves. Since the length from a leaf to a root is exactly B, the diameter of the graph is 2B.
If there exists a weighted diameter of the graph of cost 2*B, then we need to show that the cost of each chain is exactly B. Suppose it wasn’t, and the cost from the root to some leaf v is > B, let’s say B+x. Then, since there are at least 3 chains (since |A| >= 9) and since the sum of all of the weights is m*B exactly), there must exist some leaf w, with the cost of the chain from the root to w > B-x. The cost of the path from v to w is now > 2B, a contradiction.
If the cost from the root to some leaf is < B, then there must be some other leaf u with the cost from the root to u > B (since the costs of all of the edges add up to m*B), and we can do the above on u.
Since each chain costs exactly B, we can use the edge weights of each chain as the sets of 3 elements that make our 3-Partition.
Difficulty: 4. G&J does say in the comments that this problem is NP-Complete even for trees, so that may have been a hint. The proof is a little tricky (getting from “diameter ≤ K” to “set adding up to exactly K” requires some work, and there may be a more elegant way than what I did). But I think this would make a good homework problem.