This is one of my favorite problems, but one of the worst reductions to understand.  I usually skip over it when I teach it, showing them the picture of the widget and saying “See? It’s Nuts!” and moving on

The problem: Hamiltonian Circuit (HC)

The definition: Given a graph G=(V,E), where |V| = N.  Can I create an ordering <v₁, v₂…v_n>of the vertices where an edge exists between each (v_i, v_i+1) in the sequence, and the edge (v_n, v₁) also exists?

(In other words, does a sequence of edges exist that lets me start at some vertex, visit each other vertex exactly once, and return to the start?)

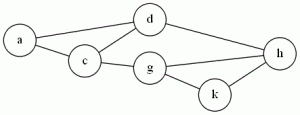
Example:

The sequence <a,d,h,k,g,c> forms a Hamiltonian Circuit

The reduction: Is from VC, and it’s nuts.  G&J do it on pages 56-60.  Starting with an instance of VC (A graph G, and an integer K), build a new graph G’ with:

• K “selector” vertices (a₁-a_k)
• 12 vertices and 14 edges (see page 57) for each edge in G (a “cover-testing” component
• Edges to connect the selector vertices to the start and end of the cover-testing component.

The Cormen algorithms book has an example of this, and it takes a graph with 4 vertices and 4 edges and builds a HC instance with 50 vertices and 72 edges.

Difficulty: 9, only because I’m sure there exist reductions that have like 25 page proofs, and I want to save my 10 for that.  But really, I think just making the students trace this reduction on an example is a really hard problem.