Tag Archives: Difficulty 8

Fault Detection With Test Points

Leave a reply

This is it! The end of the appendix!

The problem: Fault Detection with Test Points.  This is problem MS19 in the appendix.

The description: Given a directed acyclic graph G=(V,A) with one “source” vertex s with indegree 0, and one “destination” vertex t with outdegree 0, and an integer K, can we find a subset A’ of A of size K or less that induces a “test set” T:

T = \Bigl( \{s\} \cup \{u_1:(u_1,u_2) \in A'\}\Bigr) \times \Bigl( \{t\} \cup \{u_2:(u_1,u_2) \in A'\}\Bigr)

Where T has the property that for all pairs of vertices v, w \in V-{s,t}, there is some pair (u_1,u_2) \in T such that v is on a path from u_1 to u_2, but there is no path from u_1 to u_2 containing w.

What that description means:  Can I mark K or less edges so that we can use marked edges to “test” all pairs of vertices?  We “test” a pair of vertices by sending an electric signal along a path between those edges.  If a test fails (or passes), we know that something along that path has failed (or passed).  We want to be able to distinguish 2 vertices v and w by seeing if there is a test that includes v but not w (or vice versa) so that if that test fails, we can tell whether the problem is v or w, and eliminate the other possibility.

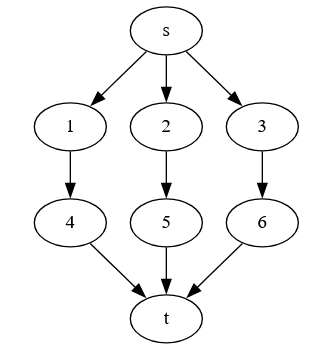
Example: It’s a little weird to create an example, because you are marking edges, and you need a path between vertices that touch marked edges.  But that path is allowed to be a single edge.  Suppose we have:

Suppose we put test points on all edges going from s, and all edges entering t.  Then we can distinguish points using these edges.  For example:

  • 1 and 2 are distinguished using the s->1 edge as a path.  (The path from s->1 includes 1 but not 2)
  • 1 and 5 are distinguished using the s->2->5->t path (the s->2 and 5->t edges).
  • 3 and 6 are distinguished using the s->3 edge as a path.

Reduction: I think this is P1 from the paper by Ibaraki, Kameda, and Toida.  They reduce from Minimum Test Set, (called “Set Distinguishibility” in the paper which is very close to what we need.

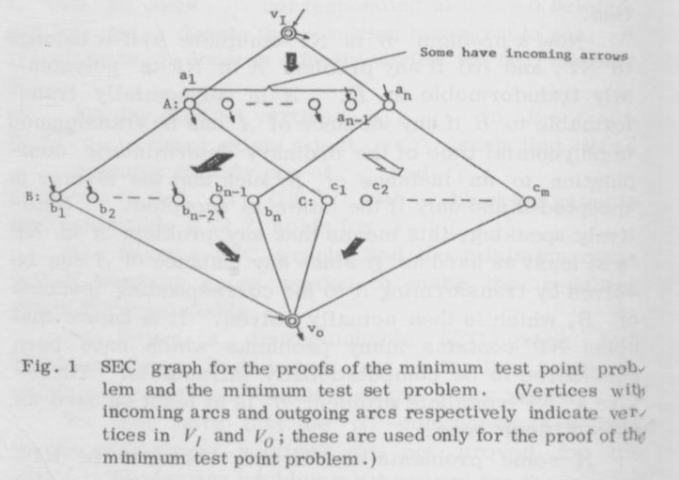
So we are given a set S of elements, and a collection C of subsets of elements.  We then build a graph.  Here it is from the paper:

A and B hold one vertex for each set in C.  C has one vertex for each element in S. The big dark arrows mean that all possible connections between those sets exist.  The big white arrow means that there is an edge from ai to cj if element j is in set i.

We will need a way to distinguish all C vertices, and can do that by placing test points on some of the edges between VI and the A vertices.  (We will be placing them on the edges that connect to vertices that will be the sets that solve the Minimum Test Set problem).

We also need to distinguish the elements of B from each other.  We’ll need new test points for that, and we can place them on the edges between the A and B vertices.

The little arrows in the picture show which edges we are putting in the test set, going into and coming out of the vertices.

Difficulty: 8  Like the last problem, I’m not sure if this is the right problem.  I also wonder why we need the B vertices at all- they don’t seem necessary for us to connect the C vertices and solve the Test Set problem.    Maybe I’m missing something?

Fault Detection in Logic Circuits

2 Replies

Just 3 problems left in the book, all to do with fault detection.

The problem: Fault Detection in Logic Circuits.  This is problem MS17 in the appendix.

The description: Given a directed graph G=(V,A) representing a circuit as follows:

  • All vertices with indegree 0 are “inputs”.  There can be several inputs.
  • Exactly one vertex, v* (called “z” in the paper), is the “output”.  This will hold the result of the circuit.
  • Each other vertex is either an AND, OR, or NOT vertex.  AND and OR vertices have indegree 2, and NOT vertices have indegree 1.

We’re given a subset V’ of V that we wish to test.  We are testing for “stuck-at” faults, where the output of the vertex is always the same regardless of the input.  Can we create a set of input tests that will detect a fault at any vertex in V’?

Example:  Here is a circuit example from the paper by Ibarra and Sahni:

‘

Our V’ is the set of y vertices, plus z (the paper uses z instead of v* to denote the output vertex).

A test set does not have to isolate which vertex is wrong.  We just want to know that if a vertex is stuck at 0 or 1, our tests will be wrong someplace.

So, a test set of setting all inputs to 1, will, if the output is 0, tell us that there is a stuck at 0 fault in one of the 4 vertices we are testing.  It will not tell us about any stuck at 1 faults, because the output should be 1 anyway.

Notice that we can’t just test setting all inputs to 0 and looking for a 1 and use that as our test to see if a stuck at 1 fault at any vertex, because the only way to get a 1 from that input would b if z itself were wrong, or if there were more than one fault, and we are only detecting single faults.  So that test only tells us about z.  In order to test the y vertices, we’ll need more tests.

If we set y1 =0, y2=1, and y3=1, the output of the circuit (and all gates) should be 0.  If we get a 1, we must have a stuck at 1 fault on y1, y4, or z.

Similarly, if we set y1=1, y2=0, and y3 = 1, an output of 1 from the circuit (instead of 0) tells us that a stuck at 1 fault is in either z, y2, or y4.

Finally, a test of y1=1, y2=1, and y3=0, and an output of 1 tells us that a stuck at one fault is in either z, y3, or y4.

Reduction: The paper by Ibarra and Sahni reduce from DNF Non-Tautology.  So we start with a formula with clauses B1..Bk, and variables x1..xn.

Each clause gets its own circuit:

The inputs xi, xj, and xk correspond to variables in the clause.  If the literal in the clause is negated, we add the not gate.  We’ve built the test set for this above (well, the version where there were no negations, but the other cases are similar).

We then hook up each of these clauses with OR gates. B1 and B2’s outputs get OR-ed together.  The output of that gets OR-ed with B3’s output, and so on.  The paper shows that once you have test sets for the inner clauses, you can test this larger circuit with 5k total tests.  First, we validate that all of these tests make at least one clause return true.  If they don’t, then we have found a way to make the formula not be a tautology, so we return “no” and stop.

Assuming we don’t have that situation we keep going and extend the circuit to something more complicated:

(This is a small example for 4 clauses.  The paper also describes a more general version)

The bottom part of the figure is the circuit we had originally for all of the clauses. The top part is fixed, and only defined by the number of clauses in the formula.

The paper proves that we can only have a legal test set for this circuit if and only if there is a way to set the variables in x so that all of the Ci circuits output 0.  If that happens, we do not have a tautology.  The idea is that if we do have a tautology, then every setting of the variables will make one of the Ci circuits output 1, and so you will never be able to detect a stuck at 1 fault in P3, since P3 will be 1 if any of the clauses output 1.  It’s a little harder to show that if we can make all of the clauses output 0, we can detect all faults, but the paper lists out how to make those tests.

Difficulty: 8.  I had a hard time following all of the circuit stuff.  I do wonder if an easier reduction is out there.