Tag Archives: Hamiltonian Circuit
Protected: Partition into Hamiltonian Subgraphs
Hamiltonian Path
Before I start doing my own problems where G&J don’t give proofs, here’s a really simple extension of Hamiltonian Circuit that will be useful.
The problem: Hamiltonian Path
The description: Given a graph G=(V,E), where |V| = N. Can I create an ordering <v1, v2…vn>of the vertices where an edge exists between each (vi, vi+1) in the sequence?
(This is the Hamiltonian Circuit problem without the restriction that I return to the start)
EDIT 4/24/15. My original reduction doesn’t work. I’ve left it below. Thanks to Fernando Berzal for pointing it out to me. I’ve added his answer, which looks correct.
In all honesty, the best part about being wrong is that it means people actually read these things!
The new Reduction: From HC. Given a graph G =(V,E), an instance of HC, pick any vertex v.
We’re going to build a graph G’ =(V’, E’)
V’ = All of the vertices in V, plus a new vertex v’ (which is a “copy” of v)
E’ = All of the edges in E, plus an edge (v’, w) if there was an edge (v,w) in E.
So, G’ is G, with one vertex (v) “duplicated” as v’. v’ has edges to all of the places v has.
We want to see if there’s an HP from v to v’.
If G’ has an HP from v to v’, then the last edge in the path goes from some vertex u to v’. If we replace that edge with the edge (u,v) we get a HC in G.
If G has an HC, then we can follow that cycle starting from v. Instead of the last edge coming back to v, follow it to v’. This will give us a HP in G’
My reduction that doesn’t work: From HC. Given a graph GHC, an instance of HC, we build GHP to be the exact same graph with 2 vertices added- vstart and vend. We add two edges, one from vstart to some vertex in GHC, and one from vend to the same vertex in GHC. The idea is that a Hamiltonian path in this graph would start at vstart, travel through the HC in the given graph (if it exists), and end at vend.
This doesn’t work because if the two new vertices both connect to the same vertex then we hit it twice in our HP, which breaks the rules.
Difficulty: 2. This is a good “simple reduction” for students to work on. I don’t use it because it’s just a variant on the same problem, and I like to drive home how reductions tie very different-looking problems together. But I do like how it’s simple, but does make you make some changes to the original problem.
(I think that I’m going to upgrade this difficulty to 4 now, since I can see a lot of students making the same mistake I did)
Hamiltonian Circuit
This is one of my favorite problems, but one of the worst reductions to understand. I usually skip over it when I teach it, showing them the picture of the widget and saying “See? It’s Nuts!” and moving on
The problem: Hamiltonian Circuit (HC)
The definition: Given a graph G=(V,E), where |V| = N. Can I create an ordering <v1, v2…vn>of the vertices where an edge exists between each (vi, vi+1) in the sequence, and the edge (vn, v1) also exists?
(In other words, does a sequence of edges exist that lets me start at some vertex, visit each other vertex exactly once, and return to the start?)
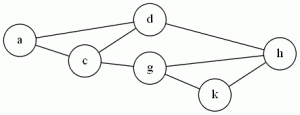
Example:
The sequence <a,d,h,k,g,c> forms a Hamiltonian Circuit
The reduction: Is from VC, and it’s nuts. G&J do it on pages 56-60. Starting with an instance of VC (A graph G, and an integer K), build a new graph G’ with:
- K “selector” vertices (a1-ak)
- 12 vertices and 14 edges (see page 57) for each edge in G (a “cover-testing” component
- Edges to connect the selector vertices to the start and end of the cover-testing component.
The Cormen algorithms book has an example of this, and it takes a graph with 4 vertices and 4 edges and builds a HC instance with 50 vertices and 72 edges.
Difficulty: 9, only because I’m sure there exist reductions that have like 25 page proofs, and I want to save my 10 for that. But really, I think just making the students trace this reduction on an example is a really hard problem.