This problem feels like a restatement of what we’ve done already
The problem: Matrix Domination. This is problem MS12 in the appendix.
The description (G&J Matrix version): Given an NxN matrix M whose entries are all 0 or 1, and a positive integer K, is there a subset C of size <= K of the rows and columns of M, such that:
- All elements of C are 1
- For all i,j, if Mij = 1 then either i or j are in C.
The description (graph version): Given a graph G=(V,E), and an integer K, is there a set of C of K edges so that each edge in the graph shares an endpoint with an edge in C?
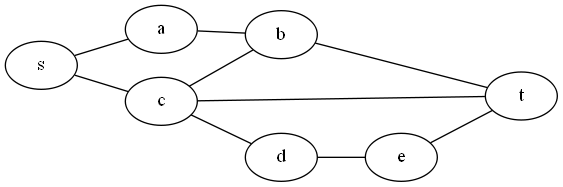
Example: Here’s a graph:
Here it is as a matrix (with row/column labels)
| s | a | b | c | d | e | t | |
| s | 0 | 1 | 0 | 1 | 0 | 0 | 0 |
| a | 1 | 0 | 1 | 0 | 0 | 0 | 0 |
| b | 0 | 1 | 0 | 1 | 0 | 0 | 0 |
| c | 1 | 0 | 1 | 1 | 0 | 0 | 1 |
| d | 0 | 0 | 0 | 1 | 0 | 1 | 0 |
| e | 0 | 0 | 0 | 0 | 1 | 0 | 1 |
| t | 0 | 0 | 1 | 1 | 0 | 1 | 0 |
If K=3, we could take edges (s,a), (c,t), and (d,e), and every edge shares an endpoint with one of those edges.
In matrix terms, we would take the elements corresponding to (s,a), (c,t), and (d,e) (and maybe their reversals), and then every 1 in the matrix shares a row or column with one of those elements.
Reduction: This feels exactly like our Minimum Maximal Matching problem. G&J reference the paper by Yannakakis and Gavril that has the reduction for that problem (there called “Edge Dominating Set”), and say that this reduction is from Minimum Maximal Matching. I don’t see that reduction (or anything relating to matrices, really) in that paper. So either I’m missing something, or the reduction is “Just represent the graph as a matrix”, which is trivial. I don’t see what I could be missing, though. Is the difference just that you have to worry about representing just the upper triangle of the matrix so you don’t have 2 entries in the matrix for each edge? That still seems really easy.
Difficulty: 1, unless I’m misunderstanding the problem.