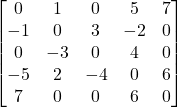Fault Detection in Logic Circuits

2 Replies

Just 3 problems left in the book, all to do with fault detection.

The problem: Fault Detection in Logic Circuits.  This is problem MS17 in the appendix.

The description: Given a directed graph G=(V,A) representing a circuit as follows:

  • All vertices with indegree 0 are “inputs”.  There can be several inputs.
  • Exactly one vertex, v* (called “z” in the paper), is the “output”.  This will hold the result of the circuit.
  • Each other vertex is either an AND, OR, or NOT vertex.  AND and OR vertices have indegree 2, and NOT vertices have indegree 1.

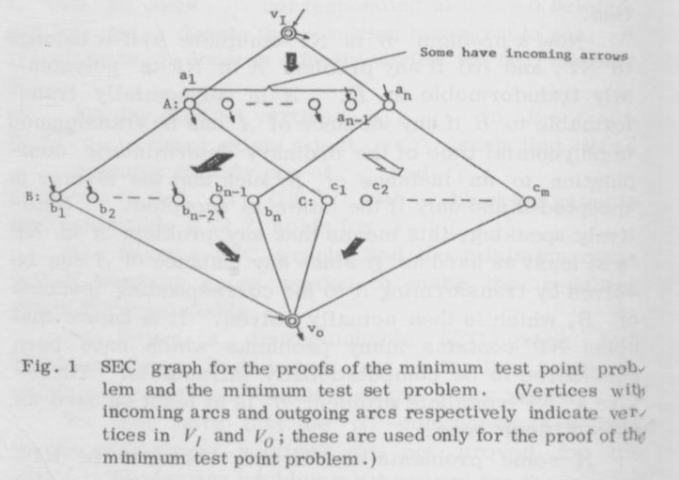
We’re given a subset V’ of V that we wish to test.  We are testing for “stuck-at” faults, where the output of the vertex is always the same regardless of the input.  Can we create a set of input tests that will detect a fault at any vertex in V’?

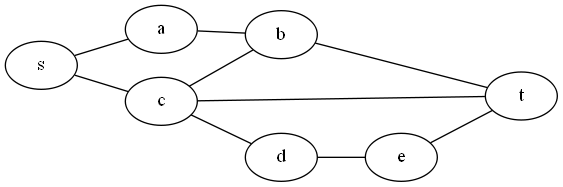
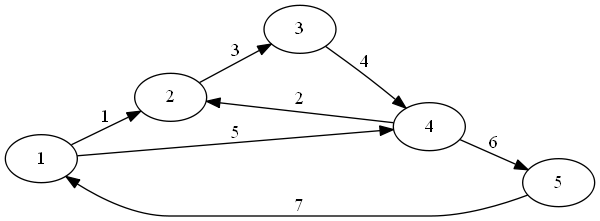
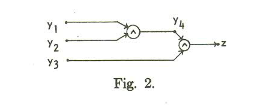
Example:  Here is a circuit example from the paper by Ibarra and Sahni:

‘

Our V’ is the set of y vertices, plus z (the paper uses z instead of v* to denote the output vertex).

A test set does not have to isolate which vertex is wrong.  We just want to know that if a vertex is stuck at 0 or 1, our tests will be wrong someplace.

So, a test set of setting all inputs to 1, will, if the output is 0, tell us that there is a stuck at 0 fault in one of the 4 vertices we are testing.  It will not tell us about any stuck at 1 faults, because the output should be 1 anyway.

Notice that we can’t just test setting all inputs to 0 and looking for a 1 and use that as our test to see if a stuck at 1 fault at any vertex, because the only way to get a 1 from that input would b if z itself were wrong, or if there were more than one fault, and we are only detecting single faults.  So that test only tells us about z.  In order to test the y vertices, we’ll need more tests.

If we set y1 =0, y2=1, and y3=1, the output of the circuit (and all gates) should be 0.  If we get a 1, we must have a stuck at 1 fault on y1, y4, or z.

Similarly, if we set y1=1, y2=0, and y3 = 1, an output of 1 from the circuit (instead of 0) tells us that a stuck at 1 fault is in either z, y2, or y4.

Finally, a test of y1=1, y2=1, and y3=0, and an output of 1 tells us that a stuck at one fault is in either z, y3, or y4.

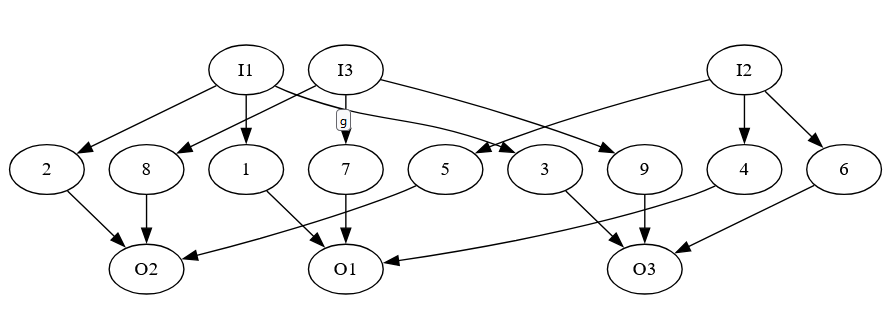
Reduction: The paper by Ibarra and Sahni reduce from DNF Non-Tautology.  So we start with a formula with clauses B1..Bk, and variables x1..xn.

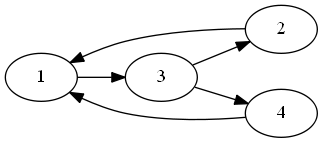
Each clause gets its own circuit:

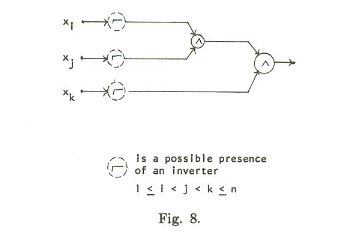
The inputs xi, xj, and xk correspond to variables in the clause.  If the literal in the clause is negated, we add the not gate.  We’ve built the test set for this above (well, the version where there were no negations, but the other cases are similar).

We then hook up each of these clauses with OR gates. B1 and B2’s outputs get OR-ed together.  The output of that gets OR-ed with B3’s output, and so on.  The paper shows that once you have test sets for the inner clauses, you can test this larger circuit with 5k total tests.  First, we validate that all of these tests make at least one clause return true.  If they don’t, then we have found a way to make the formula not be a tautology, so we return “no” and stop.

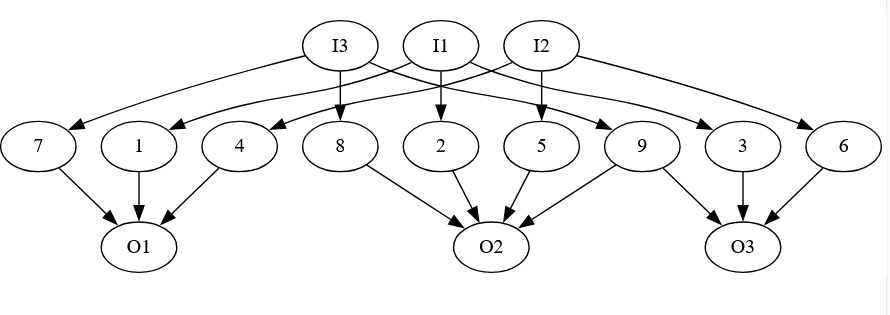
Assuming we don’t have that situation we keep going and extend the circuit to something more complicated:

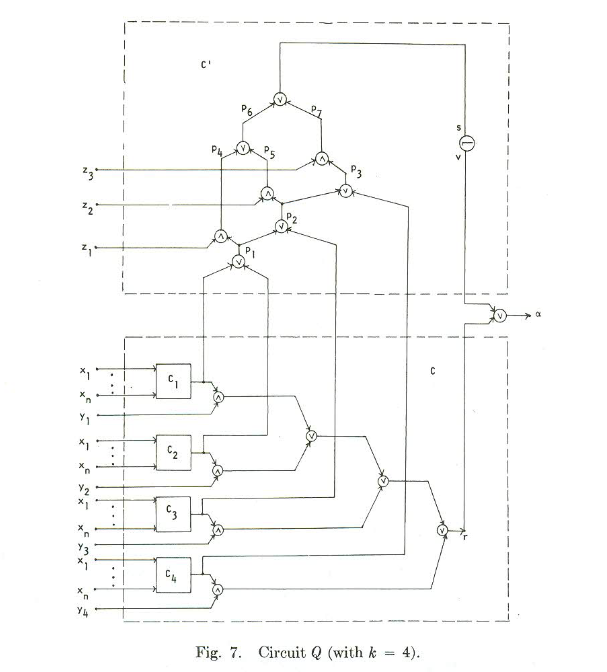
(This is a small example for 4 clauses.  The paper also describes a more general version)

The bottom part of the figure is the circuit we had originally for all of the clauses. The top part is fixed, and only defined by the number of clauses in the formula.

The paper proves that we can only have a legal test set for this circuit if and only if there is a way to set the variables in x so that all of the Ci circuits output 0.  If that happens, we do not have a tautology.  The idea is that if we do have a tautology, then every setting of the variables will make one of the Ci circuits output 1, and so you will never be able to detect a stuck at 1 fault in P3, since P3 will be 1 if any of the clauses output 1.  It’s a little harder to show that if we can make all of the clauses output 0, we can detect all faults, but the paper lists out how to make those tests.

Difficulty: 8.  I had a hard time following all of the circuit stuff.  I do wonder if an easier reduction is out there.

Minimum Weight And/Or Graph Solution

Leave a reply

This is a cool, fun reduction.  I also teach And/Or graphs in my Artificial Intelligence class, so it was fun to see this as a problem here.

The problem: Minimum Weight And/Or Graph Solution.  This is problem MS16 in the appendix.

Description: An And/Or graph is a directed, acyclic graph, where each vertex is marked as either an “and” node, or an “or” node.  We’re given a start vertex, s.  Then we “solve” the subtree at s by:

  • Solving all children of s, if s is an “and” node,
  • Or, solving one child of s, if s is an “or” node.

The solution proceeds recursively, until we get to a leaf, which can be solved directly.  Here is an example from the paper:

So, to solve P1, we could solve either P2, P3, or P7.  To solve P2, we’d need to solve both P4 and P5.

In this problem, the edges are weighted, and we’re asked: Given an integer K, is there a solution that traverses edges costing K or less?

Example: In the graph above, the cheapest solution costs 3: Solve P1 by solving P3, solve P3 by solving P6.  If P3 was an “and” node, instead of an “or” node, then the best solution would cost 4: Solve P1 by solving P2, solve P2 by solving both P4 and P5.

Reduction: Sahni’s paper has a bunch of reductions we’ve done.  This time, he uses 3SAT.  So, from a given 3SAT instance, we build a graph:

  • S is the root node, and is an “and” node
  • S has one child for each variable (x1..xn).  There is also one extra child, P.
  • Each xi is an “or” node with 2 children, one for “true”, one for “false”.   (So 2n children total)
  • Each of these 2n nodes have 1 edge coming out of it to one of the 2n leaves of the tree.
  • P is an “and” node, and has one child for each clause (C1..Ck).
  • Each clause node is an “or” node, and has 3 edges corresponding to its literals.  So if variable xi appears in clause Cj positively, there is an edge to the “true” child of xi.  If the negation ~xi appears, there is an edge to the “false” child of xi.
  • The weights of each edge are 0, except for the 1-degree edges going to the leaves, which cost 1.

To solve this graph, we need to solve S, which means we need to solve each variable (by “choosing” a truth setting for it), and we also need to solve P.  Solving P means we need to solve each clause.  Each clause is solved by choosing a truth setting for one of its literals that makes the clause true.  Since we are already choosing a truth setting for each variable, we are paying N in cost.  If we can choose setting of the variables that also solve each clause, we pay no more than N in cost, and also satisfy each clause.  If the formula is unsatisfiable, then we need to solve one variable “twice” by setting it to true and false, making us pay more than N overall.

So the formula is satisfiable if and only if the tree cost is exactly N.

Difficulty: 6.  I don’t know that I’d expect a student to come up with this themselves.  It is similar to a lot of the 3SAT reductions we’ve done, though (one “thing” per clause, one “thing” for each variable setting, connections between the clause and the settings of its literals), so if a few of these were gone over with students, maybe this could be presented along with them.

 

Decision Tree

Leave a reply

We teach decision trees in our AI and Data Analytics classes, so this is a nice problem that relates to that.

The problem: Decision Tree.  This is problem MS15 in the appendix.

The description: We’re given a set X of n objects, and a set T of tests.  Each test can be applied to each object, and returned true or false.  Can we arrange tests so that after at most K tests, we uniquely identify all objects in X?

Example: A decision tree is a way to take an unknown object and classify it into one of the elements of X.  So suppose X= {1,2,3,4}  We’ll have 3 tests:

Test 1: Is it even?

Test 2: Is the value of the number < 3?

Test 3: Does the spelling of the word have < 4 letters?

Then we could write this decision tree of height 2:

We could also use the same test in multiple nodes.  The decision trees I come across also allow for the same object from X to appear in many different leaves (because X is usually a boolean set like {Yes, No}), but the definitions here don’t seem to allow that.

Reduction: The paper from Hyafil and Rivest uses X3C.  So we’re given a set of elements X, and a collection C of 3-element subsets of X.  We’ll build a set X’ (the objects of the decision tree problem) by taking X and adding 3 new elements: {a,b,c}.  We will have 1 test in T for each triple in C (“Is our object one of these 3 elements?”).  We’ll also have 1 test for each element x in X’ (“Is our object x?”).

The paper defines a formula that we are trying to minimize for the height of the tree:

f(n) = \min_{1 \leq i \leq 3} [f(n-i) + f(i) + n] if n \geq 4

f(1) =2, f(2) = 2, f(3) = 5, f(4) = 8

So our K is f(|X’|).

We’ll want the optimal tree to look like this (picture from the paper):

The nodes in the tree above are 3-element sets from C that form the cover.  So the first node is asking “Is X in the first set of the cover?”.  If the answer is yes, we move to the right, and use the 1-element tests to figure out which of the 3 leaf nodes correspond to the exact element.  If the answer is no, we move to the left, and ask the same question of the second set in the cover.  The way to minimize the tree’s height is to have the “what 3-element set” questions be first.  We also minimize the height by making sure that each element of X’ is covered by a node in the tree- in other words, the T_{i_k} sets have to form a cover.  This means we get the minimum height (of K) from the tree if and only if we have a cover from C.

Difficulty: 6.  The reduction itself isn’t hard, but the formula is hard to see, and the paper kind of handwaves the “of course you need to be an exact cover” part of the proof.  I think if students had to do it, they’d run into some sticky issues.

Simply Deviated Disjunction

Leave a reply

This problem also uses Max-Cut, but is much harder, even to explain.

The problem: Simply Deviated Disjunction.  This is problem MS14 in the appendix.

The description: I’ve gone back and forth a lot between G&J and the paper by Pudlak and Springsteel that has the reduction, and this is my best guess at what we’re trying to do: Let’s break this down into pieces:

We’re given a collection M of n tuples, each tuple has length m.  Each element of a tuple (Mi[j] is the jth element in tuple i) has either the value 0 (meaning “false”), 1 (meaning “true”), or x (meaning “no information”).  You can think of these as attribute values in a set of data.  We’ll be doing logic operations on them, and we’ll be propogating the x’s when it potentially “matters” in the output.  So, for example, 1∨x 1, because no matter what x really is the output is 1,  but 1 ∧ x = x, because the output depends on what x is.

We then want to partition the tuples into two groups of tuples, I and J.  We can order the tuples in I and J however we want.  For each tuple, we want to know if the disjunction of all of the truth values is true or not.  (So we “or” them all together- G&J’s definition allows us to pick whether we want each row to be true or false, but the paper only cares about whether we get true values or not).  We are interested in 4 variables:

  • a: The number of rows k where the disjunction of the tuple at row k in I is true and the disjunction of the tuple at row k in J is true.
  • b: The number of rows k where the disjunction of the tuple at row k in I is true, and the disjunction of the tuple at row k in J is false.
  • c: The number of tows k where the disjunction of the tuple at row k in I is false, and the disjunction of the tuple at row k in J is true.
  • d: The number of rows k where the disjunction of the tuple at row k in I is false, and the disjunction of the tuple at row k in J is false.

It’s unclear what you do for a row that is in one of the two sets, since the sizes of the sets don’t have to be equal.  I’m assuming that will never count towards the total, but maybe it’s meant to count as false.

Anyway, the problem asks: Can we set up I and J so that ad > bc?  (This inequality is what “simply deviated” means).

Example:  Suppose I have 6 tuples, each of length 3:

  • (1,1,1)
  • (1,0,+)
  • (0,0,1)
  • (+,0,0)
  • (0,0,0)

I set up my two lists like this:

I J
(1,0,+) (1,1,1)
(0,0,1) (1,0,0)
(0,0,0) (+,0,0)

Now we calculate the letters:

 

  • a=2 (rows 1 and 2 are true in both I and J)
  • d = 1 (row 3 is not true in both I and J)
  • b and c are 0 (no row is true in one set but not true in the other)

So a*d = 2, and b*c = 0, so ad > bc

Reduction: The paper again uses the general “Max Cut” problem, which is our Bipartite Subgraph problem but where the edges have weights.  I think they would have been better off with our unweighted “Simple Max Cut” problem, as we’ll see.  So we start with a weighted graph, and a K.  Let’s call the sum of all of the weights (an edge that is not present has weight 0) wh. Here are the tuples we make:

  • m1 tuples of all zeros  (we’ll figure out how many we’ll need soon)
  • m2 tuples of all x’s (we’ll figure out how many we’ll need soon)
  • Then, for each pair of vertices (v,w) in the graph, if the weight of the edge is c, then c copies of a row of all 0’s except for a 1 corresponding to positions i and j.  (So c copies of a tuple representing the edge).

I’ll stop here to point out that this third component creates wh tuples, and since the weights of the edges are not necessarily polynomially bounded in the size of the graph, this won’t necessarily give us a polynomial time reduction.  I could be misunderstanding what they are saying.  But I also think if you use Simple Max Cut, all of the edge weights are 1 (and so wh is |E|), and we avoid this issue.

Suppose we have a cut of the vertices into two sets A and B.   We would like to set up I and J so that a is the total weight of the edges that cross the cut.  (The paper says this is a “natural correspondence”, but I’m having trouble seeing it).  If we do that, then d = m1 (the rows of all 0’s), and b+c = m2+wh -a.  I don’t exactly see where these results are coming from.  But from there, we can compute that m1 should be 1/4*wh2*(K-2) and m2 should be wh*(k-2)-wh+K-2.  This is only positive when the weight of all edges across the cut is >= K

Difficulty: 10.  I got pretty far following this, but some of the steps of the reduction I just don’t get.  I’ll say that I’m pretty sure that I’m doing something wrong, possibly with the definition of the problem, because the paper says that the two-valued problem (with no +’s) is open, and I don’t know that I’m doing anything here that isn’t the same as treating x as 0.

 

Matrix Cover

Leave a reply

I found this problem’s in Bernard Moret’s Theory of Computation Textbook, and got the reduction from the solution manual.  It was nice to see a different problem in one of those books.

The problem: Matric Cover.  This is problem MS13 in the appendix.

The description: Given an NxN matrix A, where every entry is non-negative,  and an integer K, is there a function f that maps the set {1..n} to either 1 or -1, such that

\sum_{1\leq i,j \leq n} (a_{ij}*f(i)*f(j)) \leq K?

Example: Here’s a simple matrix:

\begin{bmatrix} 5&0&2\\ 1&2&0\\ 0&3&4 \\ \end{bmatrix}

We’re trying to keep the sum of aij*f(i)*f(j) low.  My first impression was to make the function return -1 for all values. But that means we’re just adding all the aij values together (and multiplying by -1x-1=1) for a large sum.  This also means that no matter what we choose for f, all elements on the diagonal will count positively (this won’t be a problem once we use A to represent the adjacency matrix of a graph, since our graphs don’t have self-loops).  So the best we can do in this example is something like f(1)=1, f(2)=1, f(3) = -1, which gives us a sum of 5+0-2+1+2-0-0-3+4=7

Reduction: G&J and Moret both say to use Max-Cut, but since all we need is the adjacency matrix of the graph, and no weights, we can use Simple Max Cut (which we’ve been calling “Bipartite Subpgrah“).  We’re given a graph G, and an integer K, and want to know if we can find a partition of the vertices of G into two sets such that at least K edges cross between the sets.  So we’ll use the adjacency matrix of that graph as our A for Matrix Cover. We’ll set our K’ for Matrix cover to be 2(|E|-2K).  We’ll consider a function f that maps all vertices in one side of the partition as 1, and all vertices on the other side as -1.  This means that all edges that stay on the same side of the partition will contribute 1 to the sum, and all edges that cross the partition will contribute -1 to the sum.

If the Max-Cut instance is true, then there is a partition that has at least K edges cross, and so at least -K will be contributed to our sum.  At most |E|-K edges will not be cut in that case, so our total is (|E|-K)-K = |E|-2K.  We need to double this sum because the matrix is symmetric, and so edge (i,j) appears twice in the matrix.

Difficulty: 5.  I should have gotten this myself. It’s a bit tricky for a homework problem for students because of all of the details- it’s easy for example to miss the need to multiply by 2.  The fact that you don’t _make_ the f function, you just say it has to exist and have certain properties will confuse some students.     But if they know about Simple Max Cut, this is a good non-trivial one for good students.

 

Matrix Domination

Leave a reply

This problem feels like a restatement of what we’ve done already

The problem: Matrix Domination.  This is problem MS12 in the appendix.

The description (G&J Matrix version): Given an NxN matrix M whose entries are all 0 or 1, and a positive integer K, is there a subset C of size <= K of the rows and columns of M, such that:

  • All elements of C are 1
  • For all i,j, if Mij = 1 then either i or j are in C.

The description (graph version): Given a graph G=(V,E), and an integer K, is there a set of C of K edges so that each edge in the graph shares an endpoint with an edge in C?

Example: Here’s a graph:

Here it is as a matrix (with row/column labels)

s a b c d e t
s 0 1 0 1 0 0 0
a 1 0 1 0 0 0 0
b 0 1 0 1 0 0 0
c 1 0 1 1 0 0 1
d 0 0 0 1 0 1 0
e 0 0 0 0 1 0 1
t 0 0 1 1 0 1 0

If K=3, we could take edges (s,a), (c,t), and (d,e), and every edge shares an endpoint with one of those edges.

In matrix terms, we would take the elements corresponding to (s,a), (c,t), and (d,e) (and maybe their reversals), and then every 1 in the matrix shares a row or column with one of those elements.

Reduction: This feels exactly like our Minimum Maximal Matching problem.   G&J reference the paper by Yannakakis and Gavril that has the reduction for that problem (there called “Edge Dominating Set”), and say that this reduction is from Minimum Maximal Matching.  I don’t see that reduction (or anything relating to matrices, really) in that paper.  So either I’m missing something, or the reduction is “Just represent the graph as a matrix”, which is trivial.   I don’t see what I could be missing, though.  Is the difference just that you have to worry about representing just the upper triangle of the matrix so you don’t have 2 entries in the matrix for each edge?  That still seems really easy.

Difficulty: 1, unless I’m misunderstanding the problem.

Maximum Likelihood Ranking

Leave a reply

This is another (hopefully the last, we’re getting close to the end) “private communication” problem where I couldn’t find a paper to use, so I had to work through it myself, with mixed success.  Let’s see how I do.

The problem: Maximum Likelihood Ranking.  This is problem MS11 in the appendix.

The description: Suppose we have an nxn matrix A with integer values.  Further, let aij + aji = 0.  We’re also given a positive integer B.  Can we do “simultaneous row and column permutations” to A to create another matrix (G&J call it B, but I’ll call it C to avoid confusion), such that:

\sum_{1 \leq i < j \leq n} min\{b_{ij},0\} \geq -B?

The description (my interpretation): Here’s what I think that means.  You have a directed  graph with just one edge in each direction between any 2 vertices, represented as an adjacency matrix  A positive entry in the matrix is the cost to traverse the edge, and a negative entry in the matrix means you’re traversing the edge backwards.  Can I permute the rows and columns of the matrix so that the “backwards” edges in all positions where i < j sum to -B at most?”

Example: Here is a graph:

Here is its matrix:

\begin{bmatrix} 0&1&0&5&7 \\ -1&0&3&-2&0\\ 0&-3&0&4&0\\ -5&2&-4&0&6\\ 7&0&0&6&0\\ \end{bmatrix}

The negative numbers in the upper right triangle is what we are looking at to compare against our B- in this case it’s -9.

I’m pretty sure a “simultaneous row and column permutation” means you do the same permutation to the rows and to the columns.  So if the above matrix was {1,2,3,4,5}, here is {2,3,4,5,1}

\begin{bmatrix} 0&3&-2&0&-1\\ -3&0&4&0&0 \\ 2&-4&0&6&-5 \\ 0&0&-6&0&7\\ 1&0&5&-7&0\\ \end{bmatrix}

The negatives in the upper right triangle here sum to -8 (so it’s better).  It’s worth noticing that we have two cycles in the graph (2->3->4->2 and 1->4->5->1), and that any permutation will have to have a “backwards” ordering for one of the cycles.  So at least 1 edge in each cycle will have its negative value counted in our total, so this graph will be at least -7.

(Partial) Reduction: As I said, this is a “private communication” reduction, our only hint is that we are supposed to use Feedback Arc Set.  What Feedback Arc Set asks for is a set of edges that is in each directed cycle.

So, let’s try this:  Given a directed graph G=(V,E) that’s our Feedback Arc Set graph, represent it as an adjacency matrix such that aij = 1 if edge (i,j) is in E, and aij = -1 if (j,i) is in E.  Our B will be the K from the problem.

My intuition is that each cycle will have to contribute 1 edge (at least) that is negative in our upper triangle.  So if there are K edges that cover all cycles, we would get the B cost from those edges in our problem.  We want the edge in the feedback arc set to be last in the permutation order.  For example, here is a directed graph:

Here is its graph with the regular ordering:

\begin {bmatrix} 0&-1&1&-1\\ 1&0&-1&0\\ -1&1&0&0\\ 1&0&0&0\\ \end{bmatrix}

..for a cost of -3.  But we can solve the FBS instance with just 1 edge from 1-3.  So here is the matrix will all edges going forward except for that one (3,2,4,1 ordering):

\begin{bmatrix} 0&1&1&-1\\ -1&0&0&1\\ -1&0&0&0\\ 1&-1&0&0\\ \end{bmatrix}

..for a cost of -1 (because there is just 1 edge in the Feedback Arc Set)

I’d like to have my reduction be someting like “put all edges in the Feedback Arc Set in the matrix in order where they go backwards”.  But I don’t know what to do with graphs like this, where the Feedback Arc Set itself is a cycle, so you can’t do that:

{(3,4), (4,6), (6,3)} is the Feedback Arc Set here, but because it is itself a cycle, there is no permutation of vertices that will put all of the edges in the upper right.  I think this is a consequence of there being 4 cycles in the graph, but the Feedback Arc Set having just 3 edges.  But I’m not sure, and so we need to have something more in the reduction.

Difficulty: ??  It doesn’t look terribly hard, but I’m not sure what to do next.

Randomization Test For Matched Pairs

Leave a reply

This reduction gave me a lot of trouble and gave me a lot of holes to fill.  I think I filled them okay, but I’m getting the vibe that I’m missing something here- the reduction reads very differently from the way the problem is described.

The problem: Randomization Test For Matched Pairs.  This is problem MS10 in the appendix.

The description: Given a series of n pairs of integers (x1, y1) through (xn, yn), and a positive integer K.  Are there at least K subsets of the integers for which:

\sum_{i \in S} |x_i - y_i | \leq \sum_{y_i > x_i} (y_i - x_i)?

Example:  The paper by Shamos that has the reduction might have a better explanation of what we are doing: he defines zi = yi – xi, and T* to be the sum of all of the positive zi (the right side of the inequality above).  Then if we could choose some set of zi to be positive (by changing their sign), and call that sum T, are there K or more sets where T \leq T*?

So, suppose we have 4 pairs: (2,4), (1,6), (8,4), (3,2).  This would make our zi‘s {2,5,-4,-1}, and so T* would be 7.

There are 16 subsets of the above pairs (nothing seems to say that the empty set isn’t allowed).  Here are some whose T is \leq 7:

{(2,4), (1,6)}   (T=7)

{(2,4), (8,4)} (T=6)

{(2,4), (8,4), (3,2)} (T=7)

{(3,2)} (T=1)

..and so on.  A set that does not work is {(1,6), (8,4)} since its T is 9.

Reduction: Shamos uses Partition, so we are given a set of N elements.  The total sum of the elements is S, so we want two subsets of size S/2. He wants to “Perform the randomization test on the numbers” in the partition set, which I don’t get because the test needs to be done on pairs.  He also wants T* to be S/2.  The paper seems to say that you can just set that, but it has to be based on the zi.  So I came up with a way to make that happen:

For each item xi, create a pair  (xi, 0).  The zi for each of these elements will be negative.  Then add one extra pair (0. S/2).  Since this is the only positive z value, T* will be this value.  I don’t know if this is what the paper wants me to do, and I’m a little worried that adding an extra element will throw off what is next.

The paper then claims that if there is no partition of the set elements into equal-weight subsets, there are 2N-1 subsets with a T < T*.  This is because if there is no partition of equal size, then each subset of our elements either has a sum < S/2 (and this a T < T*), or its complement does.

If there is a partition, then 2 sets will have a T value of exactly T* (the two partition subsets) and half of the remaining subsets will have a T < T* as above.  So if we set K (the number of subsets whose T needs to be <= T*) to be 2N-1+2, we will have our reduction.

Difficulty: 7. I spent a long time trying to read and understand this reduction.  It’s very sparse, and, really, doesn’t explain at all how to make the pairs.  As a result, I’m pretty sure I filled in all of the holes, but it’s very possible that I’m missing something.

 

Clustering

Leave a reply

I feel a little silly I didn’t come up with this one myself.

The problem: Clustering.  This is problem MS9 in the appendix.

The description: Given a complete weighted graph G=(V,E), with a positive weight d(i,j) for each edge eij, and two positive integers K and B.  Can we partition V into K (or less) disjoint sets V1..Vk such that within each Vi, all edges that stay within the partition cost B or less?

Example: Here is a graph:

If K=2, and B=2, we could have the sets {A,C} and {B,D} as a legal cluster.  But if  K=2 and B=1, we will not be able to solve the problem.  For example, we might want to have the edges (A,B) and (A,D) in the same cluster, but that would require us also to consider the edge (B,D), which is larger than 1.

Reduction: Brucker’s paper introduces the problem using a graph, like I did above. (G&J talk about points and distances), His reduction is from Graph Coloring.

Suppose we have a coloring graph G.  We build a new graph G’ such that the weight of an edge in G’ is 1 if it did not appear in G, and its weight is 2 if it did appear in G.  Then we set out K = the K of the coloring problem (3 for 3-coloring), and B = 2.  A partition of the vertices into 3 sets where each set has no weight-2 edges is exactly a legal coloring.

Difficulty: 3.  I do think the graph terminology helps to make the problem more understandable.

Shapley-Shubik Voting Power

Leave a reply

Setting up this definition will take a bit, bear with me.

The problem: Shapley-Shubik Voting Power.  This is problem MS8 in the appendix.

The description: Suppose we have a set of n voters, each voter i has a “weight” wi, corresponding to their number of votes.  If we are doing a simple majority vote, a coalition of voters then needs votes of (strictly) more than half the sum of the weights to win.  For a specific voter i, we can look at all permutations of voters, and say that all voters before voter i in the permutation voted “yes”, and all voters after voter i in the permutation voted “no”.  We are interested in the number of these permutations where voter i’s vote “matters”- where adding voter i to the “yes” votes makes “yes” the majority, but adding them to the “no” votes makes “no” the majority.  We call voter i a pivot player if this is the case.

Is voter 1 (in the G&J definition, it’s voter N in the paper) ever a pivot?

Some clarifications:  The number of times a voter is a pivot is the “Shapley-Shubik voting power”, and the proportion of permutations the voter is a pivot (by dividing the count by N!) is the “Shapley-Shubik power index”, but all we care about here is whether the power is non-zero.

Also, the definition of the voting game (in G&J, and also in the paper) allows for a more general definition of winning, besides a simple majority- you can supply a “quota” q, and any amount of votes ≥ q is a winning coalition.  For us, q is set in the reduction to be 1/2 the sum of the weights, +1, rounded up.

Example: Suppose we had 4 voters, with weights: 5.4,3,1.  There is 13 total weight, and 7 weight is enough to win. Voter 4 has 0 coalitions in which they are the pivot (we would need 6 votes without them), so has “zero Shapley-Shubik voting power”.

If, however, we split up the same number of votes among 5 voters: 4,3,3,2,1, then the 1-vote voter can be a pivot with (among others) the 4 and the 2.  The coalition loses without our pivot voter but wins with them.

Reduction: G&J have this as an “unpublished results” problem, but luckily I found a paper by Matsui and Matsui who solved it.  So we start with Partition.  We’re given a set A of n integers.  We will create a set of weights with one weight equal to each element of A, and add one extra voter with weight 1 at the end.  This is the voter that may or may not be a pivot.

If this last voter is a pivot, then there is a coalition that needs an additional weight of 1 to become a majority.  This means the coalition had exactly half of the votes without this voter (and so the sum of the elements is a partition of A)

In the other direction, if the set has a partition, then the partition set’s votes is equal to exactly half of the votes, one short of a majority.  Adding our 1-weight voter will make it a majority, and thus that voter is a pivot.

Difficulty: 4.  This problem looks scary because the definitions of Shapley-Shubik voting power include a lot more than what you actually need to do this reduction.  Once you get past all of that, it’s actually a pretty nice problem that students can handle.