We teach decision trees in our AI and Data Analytics classes, so this is a nice problem that relates to that.

The problem: Decision Tree.  This is problem MS15 in the appendix.

The description: We’re given a set X of n objects, and a set T of tests.  Each test can be applied to each object, and returned true or false.  Can we arrange tests so that after at most K tests, we uniquely identify all objects in X?

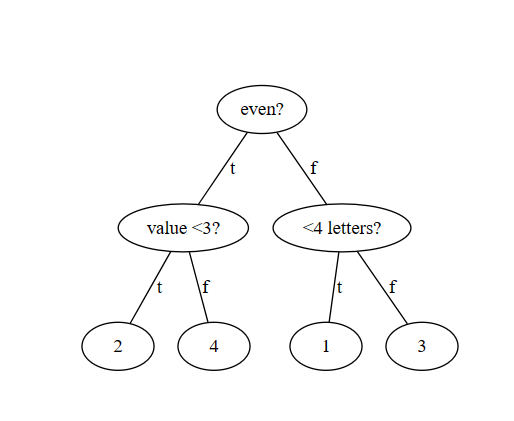
Example: A decision tree is a way to take an unknown object and classify it into one of the elements of X.  So suppose X= {1,2,3,4}  We’ll have 3 tests:

Test 1: Is it even?

Test 2: Is the value of the number < 3?

Test 3: Does the spelling of the word have < 4 letters?

Then we could write this decision tree of height 2:

We could also use the same test in multiple nodes.  The decision trees I come across also allow for the same object from X to appear in many different leaves (because X is usually a boolean set like {Yes, No}), but the definitions here don’t seem to allow that.

Reduction: The paper from Hyafil and Rivest uses X3C.  So we’re given a set of elements X, and a collection C of 3-element subsets of X.  We’ll build a set X’ (the objects of the decision tree problem) by taking X and adding 3 new elements: {a,b,c}.  We will have 1 test in T for each triple in C (“Is our object one of these 3 elements?”).  We’ll also have 1 test for each element x in X’ (“Is our object x?”).

The paper defines a formula that we are trying to minimize for the height of the tree:

if

So our K is f(|X’|).

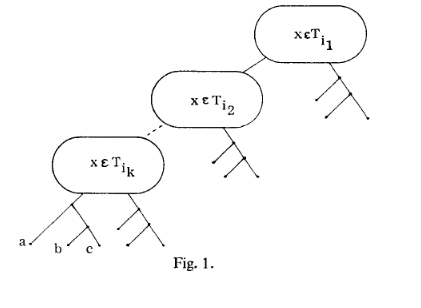
We’ll want the optimal tree to look like this (picture from the paper):

The nodes in the tree above are 3-element sets from C that form the cover.  So the first node is asking “Is X in the first set of the cover?”.  If the answer is yes, we move to the right, and use the 1-element tests to figure out which of the 3 leaf nodes correspond to the exact element.  If the answer is no, we move to the left, and ask the same question of the second set in the cover.  The way to minimize the tree’s height is to have the “what 3-element set” questions be first.  We also minimize the height by making sure that each element of X’ is covered by a node in the tree- in other words, the sets have to form a cover.  This means we get the minimum height (of K) from the tree if and only if we have a cover from C.

Difficulty: 6.  The reduction itself isn’t hard, but the formula is hard to see, and the paper kind of handwaves the “of course you need to be an exact cover” part of the proof.  I think if students had to do it, they’d run into some sticky issues.