Tag Archives: Difficulty 7

Fault Detection in Directed Graphs

Leave a reply

Let’s see if I can finish out these last few problems.

The problem: Fault Detection in Directed Graphs. This is problem MS18 in the appendix

The description: Given a directed, acyclic graph G=(V,A).  We denote the set I as the set of vertices with indegree 0, and the set O as the set of vertices of outdegree 0.  Given an integer K, can we find a set of K or less paths starting at a vertex in I, and ending at a vertex in O, where every vertex in V is on at least one of those paths?

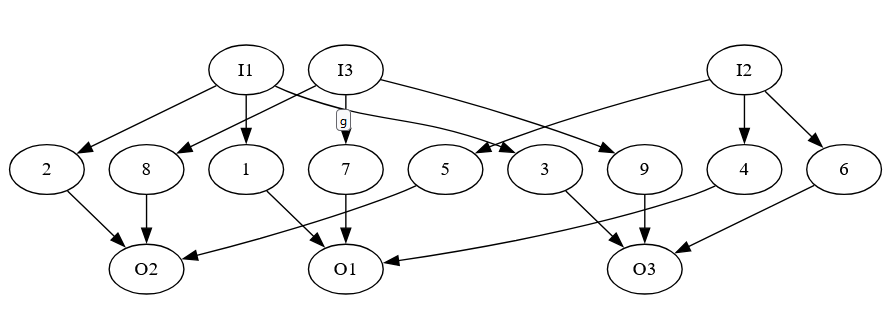
Example: It took me a long time to wrap my head around this, and I’m still not 100% convinced the version in the paper is this problem.  But here is an example that I think is helpful:

Notice that each of the middle vertices is on a separate path from an I vertex to an O vertex.  So, we will need all 9 combinations (from every I vertex to every O vertex) to ensure that all middle vertices are covered.

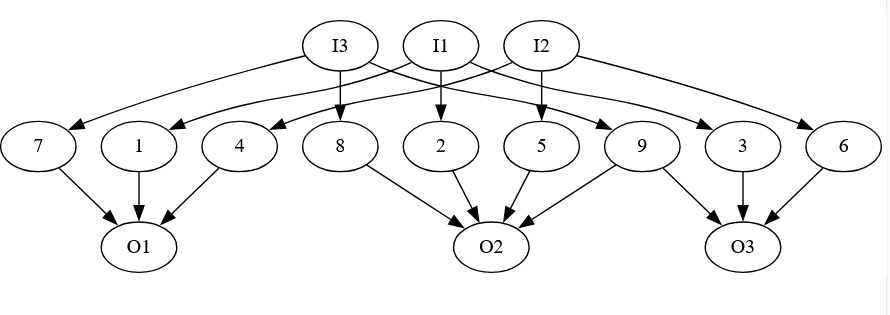
But now, suppose we add one more edge from 9 to O2:

Now we don’t need a separate start and end from I3 to O3, since there is a path  from I3 to 02, choosing that pair as a start/end combination will give us paths that cover both vertex 8 and vertex 9.

Reduction: The paper by Ibaraki, Kameda, and Toida write the problem a bit differently, and they have a lot of different problems in their paper, and to be honest, I’m not sure which one is for this problem.  (I think it’s P3?  But their reduction seems to have extra stuff that we don’t need).

So, I’m going to try to do the reduction myself from X3C, like G&J suggest in the appendix, but take inspiration for how the structure is built from the paper.

To do this, I really want a version of this problem where we only care about paths through internal nodes (vertices not in I or O).  So, it’s possible that a vertex in I or O is not in a path, but every vertex not in I or O is in some path.  We can reduce this to the real version by creating extra “dummy” vertices that are internal:  For each vertex ij ∈ I, create a vertex aj, and an edge ij → aj, and replace all other edges exiting ij with corresponding edges leaving aj instead.  We can do the same thing with O by placing vertices “before” the O vertices.  That way the only way to have a path through those new internal vertices is to have a path through all I and O vertices as well.

For our real reduction, we start with an X3C instance- a set of elements X (|X| = 3q, for some positive q), and a collection C of 3-element subsets of X.  Both our I set and our O set will have one vertex for each element of C (so 2 copies of all elements total).  In between, we will create a set of vertices X, one vertex for each element of X.  We will have edges from each I vertex (a subset)  to the 3 X (element) vertices it is a part of, and from each X vertex to the O vertices it is a part of.  Set K’ = K.

If we have an X3C instance, then choosing the sets in the solution as the I and O elements, and making them pairs, will give us a cover of all of the X elements in the middle.

If we have a cover of size K, then if we have the same sets in both the I and the O sets (so both “sides” agree on what sets to use), we clearly have an X3C solution.  It’s possible, though, that there is some pair (Ia, Ob) where a != b.  However, we know that:

  • Each element in X is along some path from an I vertex to an O vertex
  • We need K pairs of elements to make the cover, and we have 3K elements to cover.overall, and so each element in X is a member of exactly one path from an I vertex to an O vertex.
  • So, each element in X occurs in exactly one I vertex in some pair in the solution.  (And, each I vertex occurs at most once in some pair)
  • Thus, just taking all of the sets corresponding to the I vertices gives us an X3C solution
  • (And, relatedly, we can shift the O vertices to be the corresponding sets to the I vertices and remain a cover of the internal vertices).

Difficulty: 7.  I’m still not entirely sure I am talking about the right problem from the paper.  It also took me a lot of time to come up with the reduction, because X3C wants us to choose some, but not all, of the sets in the collection, but the whole point of this problem is that we can leave things out.  I played with an idea where all of the vertices connected to each other 3 times, but couldn’t make it work.  Hopefully this version makes more sense.

 

Randomization Test For Matched Pairs

Leave a reply

This reduction gave me a lot of trouble and gave me a lot of holes to fill.  I think I filled them okay, but I’m getting the vibe that I’m missing something here- the reduction reads very differently from the way the problem is described.

The problem: Randomization Test For Matched Pairs.  This is problem MS10 in the appendix.

The description: Given a series of n pairs of integers (x1, y1) through (xn, yn), and a positive integer K.  Are there at least K subsets of the integers for which:

\sum_{i \in S} |x_i - y_i | \leq \sum_{y_i > x_i} (y_i - x_i)?

Example:  The paper by Shamos that has the reduction might have a better explanation of what we are doing: he defines zi = yi – xi, and T* to be the sum of all of the positive zi (the right side of the inequality above).  Then if we could choose some set of zi to be positive (by changing their sign), and call that sum T, are there K or more sets where T \leq T*?

So, suppose we have 4 pairs: (2,4), (1,6), (8,4), (3,2).  This would make our zi‘s {2,5,-4,-1}, and so T* would be 7.

There are 16 subsets of the above pairs (nothing seems to say that the empty set isn’t allowed).  Here are some whose T is \leq 7:

{(2,4), (1,6)}   (T=7)

{(2,4), (8,4)} (T=6)

{(2,4), (8,4), (3,2)} (T=7)

{(3,2)} (T=1)

..and so on.  A set that does not work is {(1,6), (8,4)} since its T is 9.

Reduction: Shamos uses Partition, so we are given a set of N elements.  The total sum of the elements is S, so we want two subsets of size S/2. He wants to “Perform the randomization test on the numbers” in the partition set, which I don’t get because the test needs to be done on pairs.  He also wants T* to be S/2.  The paper seems to say that you can just set that, but it has to be based on the zi.  So I came up with a way to make that happen:

For each item xi, create a pair  (xi, 0).  The zi for each of these elements will be negative.  Then add one extra pair (0. S/2).  Since this is the only positive z value, T* will be this value.  I don’t know if this is what the paper wants me to do, and I’m a little worried that adding an extra element will throw off what is next.

The paper then claims that if there is no partition of the set elements into equal-weight subsets, there are 2N-1 subsets with a T < T*.  This is because if there is no partition of equal size, then each subset of our elements either has a sum < S/2 (and this a T < T*), or its complement does.

If there is a partition, then 2 sets will have a T value of exactly T* (the two partition subsets) and half of the remaining subsets will have a T < T* as above.  So if we set K (the number of subsets whose T needs to be <= T*) to be 2N-1+2, we will have our reduction.

Difficulty: 7. I spent a long time trying to read and understand this reduction.  It’s very sparse, and, really, doesn’t explain at all how to make the pairs.  As a result, I’m pretty sure I filled in all of the holes, but it’s very possible that I’m missing something.