Tag Archives: uncited reduction
Protected: Minimum Edge-Cost Flow
Monotone 3-Satisfiability
I told Daniel when he gave me his Monotone Satisfiability reduction that the actual problem mentioned in G&J was Monotone 3-Satisfiability. So he went off and did that reduction too.
The Problem:
Monotone 3 SAT. This is a more restrictive case of Monotone SAT
The Description:
Given an formula of clauses ![]() where each clause in
where each clause in ![]() contains all negated or non-negated variables, and each clause
contains all negated or non-negated variables, and each clause ![]() contains at most
contains at most ![]() variables. Does there exist an assignment of the variables so that
variables. Does there exist an assignment of the variables so that ![]() is satisfied?
is satisfied?
Example:
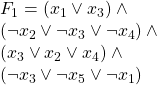
the following assignment satisfies ![]() :
:
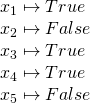
However:
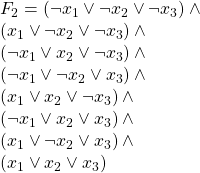
And the following is ![]() in Monotone 3SAT form:
in Monotone 3SAT form:
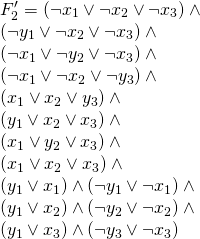
are both unsatisfiable.
The reduction:
In the following reduction we are given an instance of 3SAT,
![]() . Here each clause is of the form:
. Here each clause is of the form:
![]() where
where
![]()
and each ![]() is a literal of the form
is a literal of the form ![]() .
.
We use the following construction to build an instance of Monotone 3 SAT out of the above instance of 3SAT :
In each clause ![]() we have at most one literal,
we have at most one literal, ![]() that is not of the same parity as the rest of the literals in the clause. For every such literal, we may preform the following substitution:
that is not of the same parity as the rest of the literals in the clause. For every such literal, we may preform the following substitution:
![]() this yields a modified clause
this yields a modified clause ![]() .
.
Now we must be able to guarantee that ![]() and
and ![]() are mapped to opposite truth values, so we introduce the new clause:
are mapped to opposite truth values, so we introduce the new clause:
![]() and conjunct it onto our old formula
and conjunct it onto our old formula ![]() producing a new formula
producing a new formula ![]() .
.
For example:
![]() so we preform the substitution
so we preform the substitution
![]()
so ![]() and
and ![]()
Now repeating this procedure will result in a new formula: ![]() .
.
We claim logical equivalence between the ![]() and
and ![]() This is semantically intuitive as the
This is semantically intuitive as the ![]() clause requires all substituted literal
clause requires all substituted literal ![]() in
in ![]() to take the value opposite of
to take the value opposite of ![]() this was the stipulation for the substitution initially. It is also verifiable by truth table construction for:
this was the stipulation for the substitution initially. It is also verifiable by truth table construction for:
![]()
![]() :
:
If there exists a truth assignment ![]() that satisfies
that satisfies ![]() , then we may extent this truth assignment to produce
, then we may extent this truth assignment to produce ![]() which will satisfy
which will satisfy
![]() by letting
by letting ![]() for all
for all ![]() and letting
and letting ![]() for all
for all ![]() .
.
Obviously if ![]() is satisfiable
is satisfiable ![]() must be by the above construction of
must be by the above construction of ![]() . So by the above claim we have that
. So by the above claim we have that ![]() will satisfy
will satisfy ![]() .
.
![]() :
:
Continuing from the above, if we have a truth assignment ![]() that satisfies
that satisfies ![]() , then by the claim above it also must satisfy
, then by the claim above it also must satisfy ![]() . And
. And ![]() is a sub-formula of
is a sub-formula of ![]() so any truth assignment that satisfies
so any truth assignment that satisfies ![]() must also satisfy
must also satisfy ![]() .
.
(Back to me)
Difficulty: 4, since it’s a little harder than the regular Monotone Sat one.
Protected: Kth Shortest Path
Monotone Satisfiability
This semester I’m doing an independent study with a student, Daniel Thornton, looking at NP-Complete problems. He came up with a reduction for Monotone Satisfiability, and since I hadn’t gotten to that problem yet, I told him if he wrote it up, I’d post it.
So, here it is. Take it away, Daniel!
The Problem: Monotone SAT. This is mentioned in problem LO2 in the book.
The description:
Given an set of clauses ![]() where each clause in F contains all negated or non-negated variables, is there an assignment of the variables so that
where each clause in F contains all negated or non-negated variables, is there an assignment of the variables so that ![]() is satisfied?
is satisfied?
Example:
![]()
the following assignment satisfies ![]() :
:
![]()
![]()
![]()
![]()
The reduction:
In the following reduction we are given an instance of SAT, with the clauses:
![]() . Here each clause is of the form
. Here each clause is of the form ![]() and each
and each ![]() is a literal of the form
is a literal of the form ![]()
Now we build an instance of Monotone SAT from the instance of SAT given above:
For each ![]() we construct two new clauses
we construct two new clauses ![]() and
and ![]() , such that all elements of
, such that all elements of ![]() are non-negated literals and all terms in
are non-negated literals and all terms in ![]() are negated literals with the addition of the new special term
are negated literals with the addition of the new special term ![]() . Now let us build a new formula
. Now let us build a new formula ![]() this is our instance of Monotone SAT, clauses are either all non-negated or negated.
this is our instance of Monotone SAT, clauses are either all non-negated or negated.
![]() :
:
Notice how we added the extra literal ![]() or
or ![]() to each of the clauses
to each of the clauses ![]() or
or ![]() respectfully. Now if there is an assignment that satisfies all of the clauses of
respectfully. Now if there is an assignment that satisfies all of the clauses of ![]() then as only
then as only ![]() or
or ![]() may be satisfied by the appended extra literal, one of the clauses must be satisfied by it’s other literals. These literals are also in
may be satisfied by the appended extra literal, one of the clauses must be satisfied by it’s other literals. These literals are also in ![]() so such an assignment satisfies all
so such an assignment satisfies all ![]() .
.
![]() :
:
Using an argument similar to the one above, For ![]() to be satisfied there must be at least one literal assignment say
to be satisfied there must be at least one literal assignment say ![]() that satisfies each clause
that satisfies each clause ![]() Now
Now ![]() is in either
is in either ![]() or
or ![]() . This implies that at least one of
. This implies that at least one of ![]() or
or ![]() is also satisfied by
is also satisfied by ![]() , so simply assign the new term
, so simply assign the new term ![]() accordingly to satisfy the clause in
accordingly to satisfy the clause in ![]() not satisfied by
not satisfied by ![]()
(back to me again)
Difficulty: 3. I like that the reduction involves manipulating the formula, instead of applying logical identities.