Tag Archives: Vertex Cover
Protected: Feedback Vertex Set
Hamiltonian Circuit
This is one of my favorite problems, but one of the worst reductions to understand. I usually skip over it when I teach it, showing them the picture of the widget and saying “See? It’s Nuts!” and moving on
The problem: Hamiltonian Circuit (HC)
The definition: Given a graph G=(V,E), where |V| = N. Can I create an ordering <v1, v2…vn>of the vertices where an edge exists between each (vi, vi+1) in the sequence, and the edge (vn, v1) also exists?
(In other words, does a sequence of edges exist that lets me start at some vertex, visit each other vertex exactly once, and return to the start?)
Example:
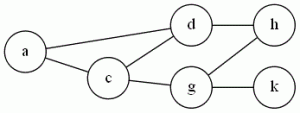
The sequence <a,d,h,k,g,c> forms a Hamiltonian Circuit
The reduction: Is from VC, and it’s nuts. G&J do it on pages 56-60. Starting with an instance of VC (A graph G, and an integer K), build a new graph G’ with:
- K “selector” vertices (a1-ak)
- 12 vertices and 14 edges (see page 57) for each edge in G (a “cover-testing” component
- Edges to connect the selector vertices to the start and end of the cover-testing component.
The Cormen algorithms book has an example of this, and it takes a graph with 4 vertices and 4 edges and builds a HC instance with 50 vertices and 72 edges.
Difficulty: 9, only because I’m sure there exist reductions that have like 25 page proofs, and I want to save my 10 for that. But really, I think just making the students trace this reduction on an example is a really hard problem.
Independent Set
The last of the three similar graph problems, it’s also probably the easiest reduction. When I teach NP-Completeness, I’ve had a lot of success starting with this reduction (instead of building a stable of NP-Complete problems from zero like the textbooks do). You kind of have to say “Trust me, Vertex Cover is NP-Complete, I’ll show you why later”, but starting with a simple reduction means that they can follow the idea and the process right from the beginning without having to be bogged down in ugly conversions involving SAT.
The problem: Independent Set (IS)
The definition Given a graph G=(V,E) and an integer J. Does G have a collection of at least J vertices where no edges connect any two vertices in J?
Example: Using the same graph:
{a,h,k} is an independent set of size 3.
The reduction: From VC. Use the exact same graph, and set J=|V|-K. (G has an independent set of J vertices exactly when it has a vertex cover of K vertices. Vertices not in the cover can’t have edges between them).
Difficulty: 1. There’s a reason why I do this first (though sometimes I go from Clique instead). In general, though, I try to avoid making them do problems that are too easy for homeworks and tests. If the reduction is trivial, it makes showing that the conversion solves the original problem difficult. You get a lot of proofs that basically say “C’mon! They’re the same thing!”. Which is not what I’m looking for 🙂
Clique
G&J don’t even bother to prove Clique is NP-Complete, just stating that it (and Independent Set) is a “different version” of Vertex Cover. But the problem comes up often enough that it’s worth seeing in its own right.
The problem: Clique (I’ve also seen “Max Clique” or “Clique Decision Problem” (CDP))
The definition: Given a graph G=(V,E), and a positive integer J (G&J say J needs to be ≤ |V|, but I think you can allow large values and make your algorithm just say “no”). Does J contain a subset V’ of V, or size at least J, where every two vertices in V’ are joined by an edge in E?
Example: Using the graph we had for VC:
{a,c,d} form a clique of size 3. There are no cliques of size 4, but if we add the edge (d,g) and the edge (c,h), then the vertices {c,d,g,h} would be one.
The reduction: From Vertex Cover. Given a graph G and an integer K that is an instance of Vertex Cover, take the complement of G (the complement of a graph has the same vertices, but the set of edges is “inverted”: (u,v) is an edge in the complement if and only if it was not an edge in G), and use it as your instance of CDP. Set J= |V|-K
Difficulty: 3. It’s not a 2 because it takes a little thought to see why the complement works.
Note: As stated perviously, I teach this course using the Cormen book, so in class I show Clique is NP-Hard by reducing from 3SAT. It’s a good example of a hard reduction, probably about as hard as the VC reduction G&J do.
Vertex Cover
Back to the “core 6” with a classic problem from graph theory. There are lots of similar graph problems, so it’s important to keep them all straight.
The Problem: Vertex Cover (VC)
The Definition: Given a graph G=(V,E) and a positive integer K (G&J say that K ≤ |V|, but really, if it’s bigger than that, you can have the algorithm just return “yes”). Can I find a subset V’ of V, |V’| ≤ K, where every edge in E has at least one endpoint in V’?
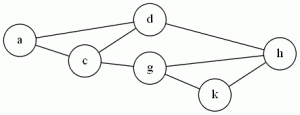
Example: Hmm, I wonder if I can insert an image..
Ok, looks like that worked. In the graph above, {c,d,g} is a vertex cover, because all edges have at least one endpoint in the set {c,d,g}. As we’ll see later, a graph containing a clique (complete subgraph) of N nodes will need at have at least N-1 of those vertices in the cover.
The reduction: From 3SAT. G&J on pages 54-56 show the construction. We build a graph with vertices for all variables and their negation, with an edge between them. We have three variables for each clause, connected in a triangle. (The three variables correspond to “positions” in the clause). Then there is an edge from each vertex corresponding to a literal (or its negation) to its corresponding “clause vertex”- the vertex that holds the position of that variable in the original formula. K= # of variables + 2* number of clauses.
Difficulty: 7 , assuming it’s the first time a student has seen this sort of reduction. If they have seen something similar (for example, a reduction from 3SAT to Clique), then maybe a 5. The ideas are pretty similar.
Note: I teach my algorithms class using the Cormen book. In it, they reduce 3SAT to Clique, proving Clique is NP-Complete, and then reduce Clique to VC. This works in the exact same way as the reduction from VC to Clique that I’ll be doing here next.